Differentially Private Quantiles

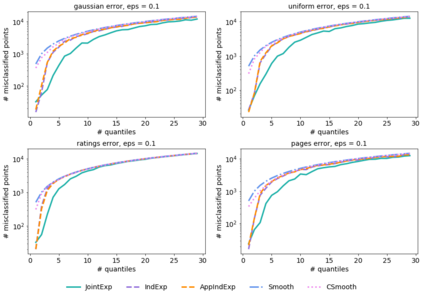
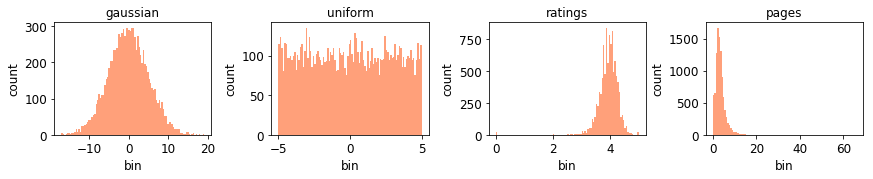
Quantiles are often used for summarizing and understanding data. If that data is sensitive, it may be necessary to compute quantiles in a way that is differentially private, providing theoretical guarantees that the result does not reveal private information. However, in the common case where multiple quantiles are needed, existing differentially private algorithms scale poorly: they compute each quantile individually, splitting their privacy budget and thus decreasing accuracy. In this work we propose an instance of the exponential mechanism that simultaneously estimates $m$ quantiles from $n$ data points while guaranteeing differential privacy. The utility function is carefully structured to allow for an efficient implementation that avoids exponential dependence on $m$ and returns estimates of all $m$ quantiles in time $O(mn^2 + m^2n)$. Experiments show that our method significantly outperforms the current state of the art on both real and synthetic data while remaining efficient enough to be practical.