Translation invariant diagonal frame decomposition for the Radon transform

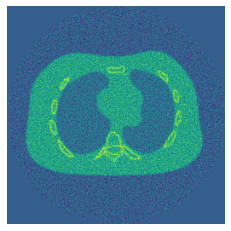
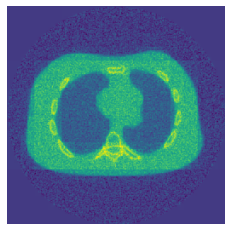
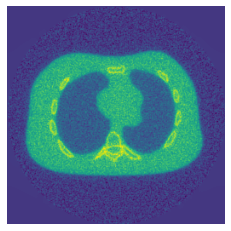
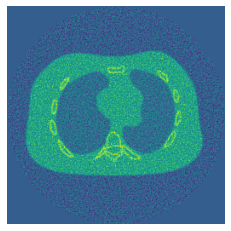
In this article, we address the challenge of solving the ill-posed reconstruction problem in computed tomography using a translation invariant diagonal frame decomposition (TI-DFD). First, we review the concept of a TI-DFD for general linear operators and the corresponding filter-based regularization concept. We then introduce the TI-DFD for the Radon transform on $L^2(\R^2)$ and provide an exemplary construction using the TI wavelet transform. Presented numerical results clearly demonstrate the benefits of our approach over non-translation invariant counterparts.