Overcoming bias in representational similarity analysis

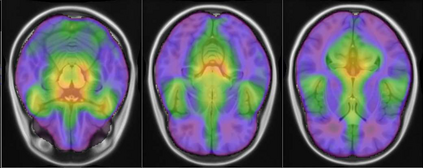
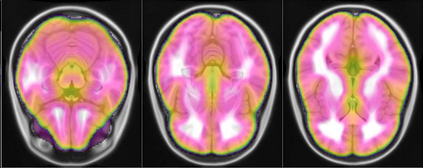
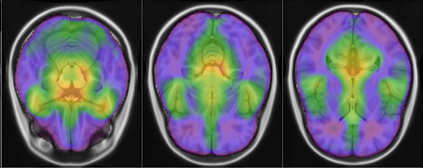
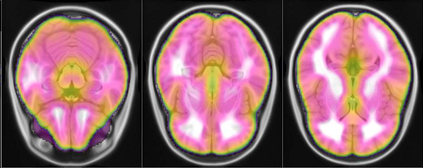
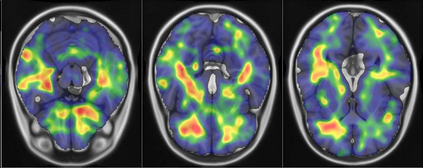
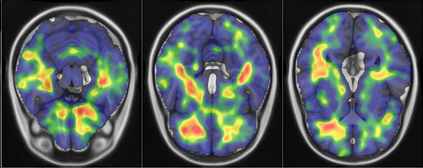
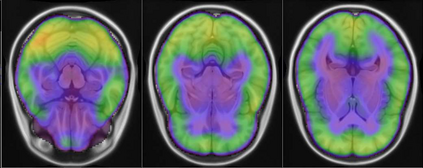
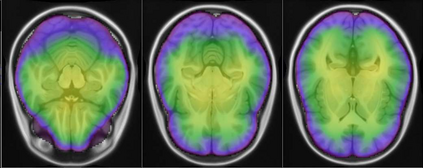
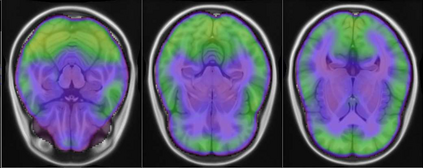
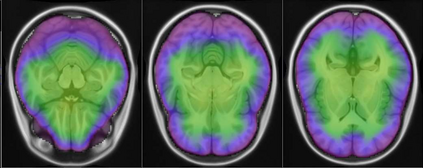
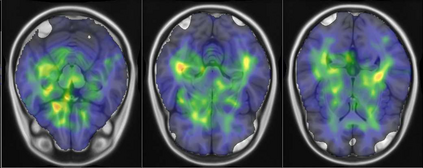
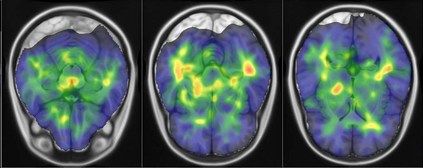
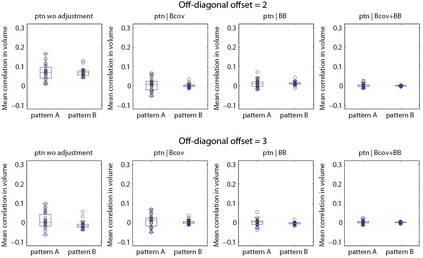
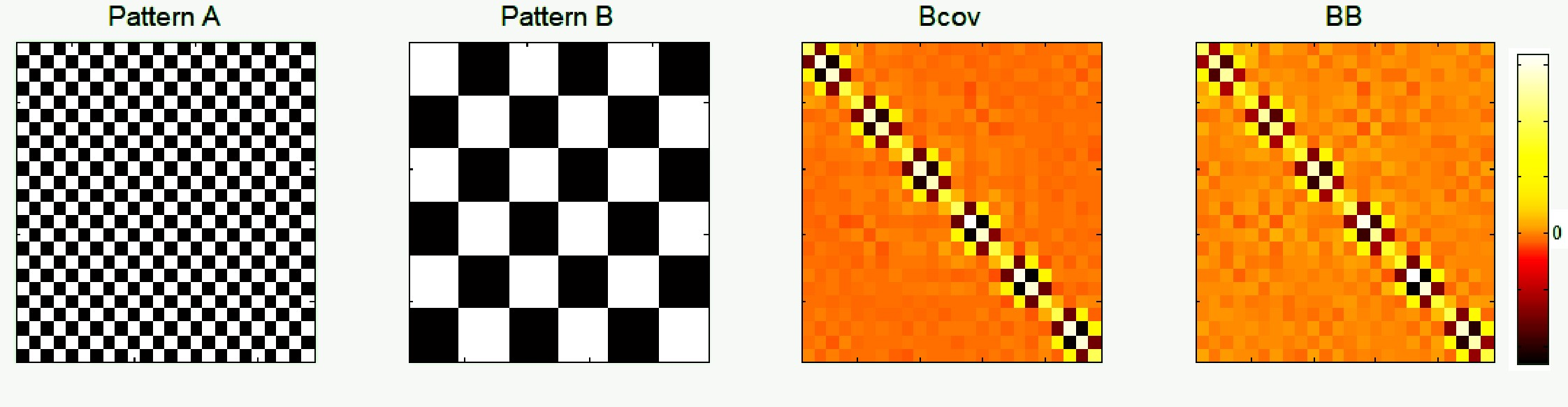
Representational similarity analysis (RSA) is a multivariate technique to investigate cortical representations of objects or constructs. While avoiding ill-posed matrix inversions that plague multivariate approaches in the presence of many outcome variables, it suffers from the confound arising from the non-orthogonality of the design matrix. Here, a partial correlation approach will be explored to adjust for this source of bias by partialling out this confound. A formal analysis will show the dependence of this confound on the temporal correlation model of the sequential observations, motivating a data-driven approach that avoids the problem of misspecification of this model. However, where the autocorrelation locally diverges from the volume average, bias may be difficult to control for exactly (local bias), given the difficulties of estimating the precise form of the confound at each voxel. Application to real data shows the effectiveness of the partial correlation approach, suggesting the impact of local bias to be minor. However, where the control for bias locally fails, possible spurious associations with the similarity matrix of the stimuli may emerge. This limitation may be intrinsic to RSA applied to non-orthogonal designs.