Online Target Q-learning with Reverse Experience Replay: Efficiently finding the Optimal Policy for Linear MDPs

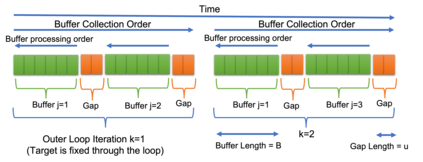
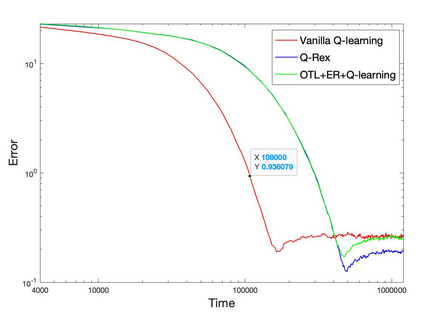
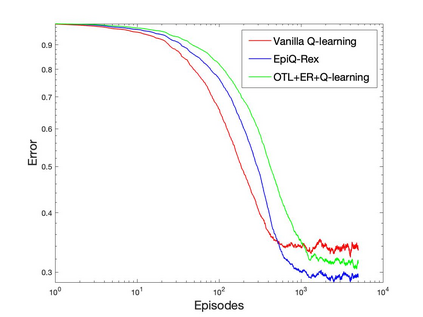
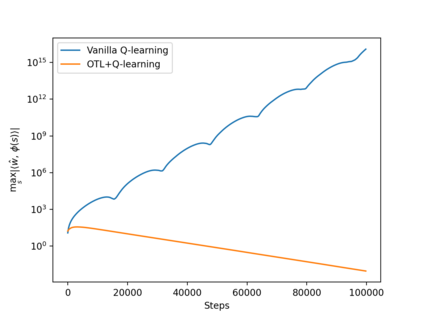
Q-learning is a popular Reinforcement Learning (RL) algorithm which is widely used in practice with function approximation (Mnih et al., 2015). In contrast, existing theoretical results are pessimistic about Q-learning. For example, (Baird, 1995) shows that Q-learning does not converge even with linear function approximation for linear MDPs. Furthermore, even for tabular MDPs with synchronous updates, Q-learning was shown to have sub-optimal sample complexity (Li et al., 2021;Azar et al., 2013). The goal of this work is to bridge the gap between practical success of Q-learning and the relatively pessimistic theoretical results. The starting point of our work is the observation that in practice, Q-learning is used with two important modifications: (i) training with two networks, called online network and target network simultaneously (online target learning, or OTL) , and (ii) experience replay (ER) (Mnih et al., 2015). While they have been observed to play a significant role in the practical success of Q-learning, a thorough theoretical understanding of how these two modifications improve the convergence behavior of Q-learning has been missing in literature. By carefully combining Q-learning with OTL and reverse experience replay (RER) (a form of experience replay), we present novel methods Q-Rex and Q-RexDaRe (Q-Rex + data reuse). We show that Q-Rex efficiently finds the optimal policy for linear MDPs (or more generally for MDPs with zero inherent Bellman error with linear approximation (ZIBEL)) and provide non-asymptotic bounds on sample complexity -- the first such result for a Q-learning method for this class of MDPs under standard assumptions. Furthermore, we demonstrate that Q-RexDaRe in fact achieves near optimal sample complexity in the tabular setting, improving upon the existing results for vanilla Q-learning.