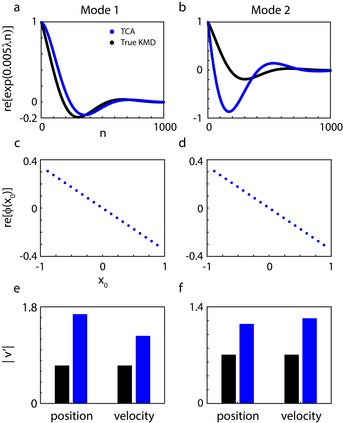
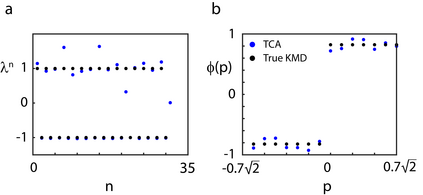
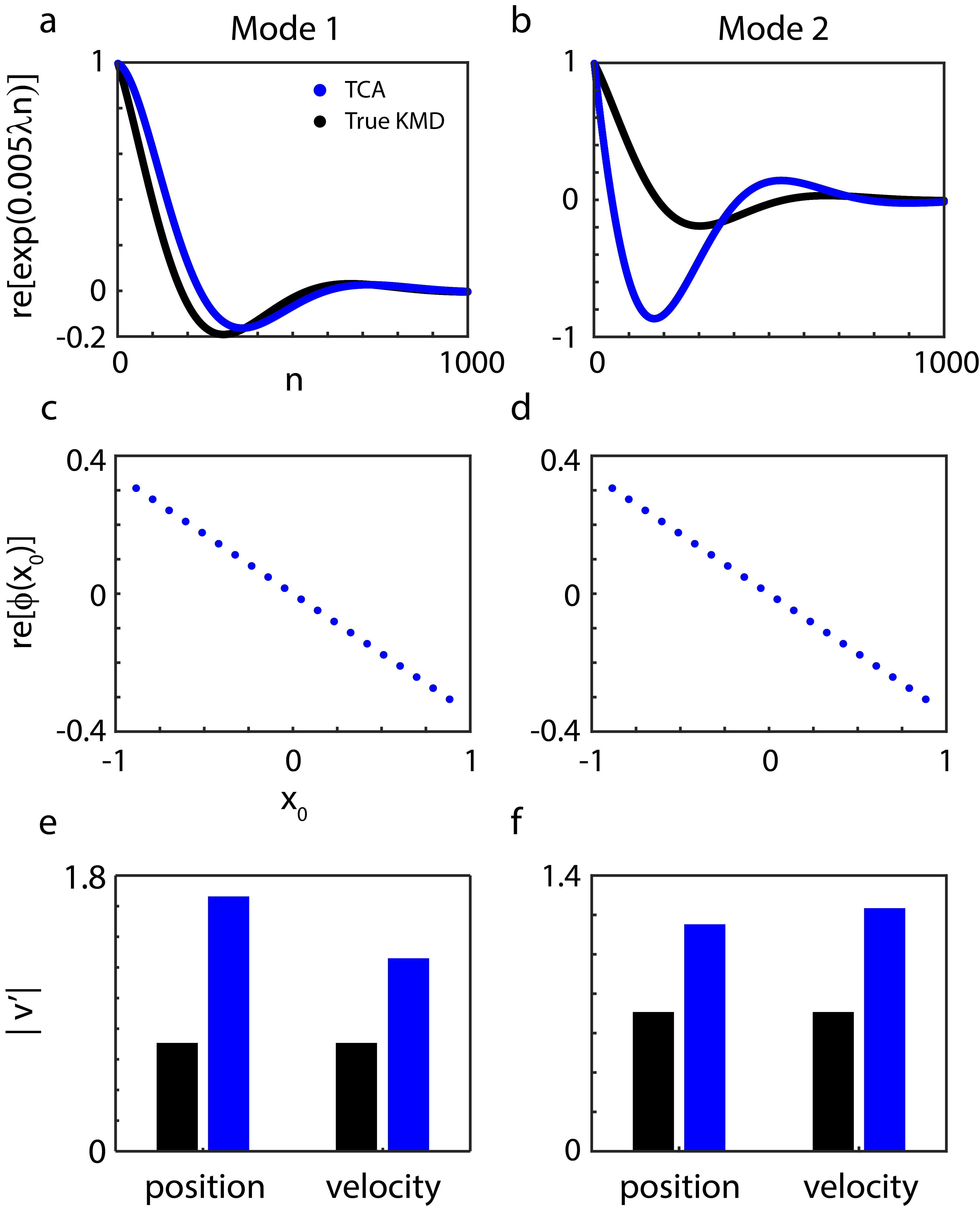
Koopman mode decomposition and tensor component analysis (also known as CANDECOMP/PARAFAC or canonical polyadic decomposition) are two popular approaches of decomposing high dimensional data sets into low dimensional modes that capture the most relevant features and/or dynamics. Despite their similar goal, the two methods are largely used by different scientific communities and formulated in distinct mathematical languages. We examine the two together and show that, under a certain (reasonable) condition on the data, the theoretical decomposition given by tensor component analysis is the \textit{same} as that given by Koopman mode decomposition. This provides a "bridge" with which the two communities should be able to more effectively communicate. When this condition is not met, Koopman mode decomposition still provides a tensor decomposition with an \textit{a priori} computable error, providing an alternative to the non-convex optimization that tensor component analysis requires. Our work provides new possibilities for algorithmic approaches to Koopman mode decomposition and tensor component analysis, provides a new perspective on the success of tensor component analysis, and builds upon a growing body of work showing that dynamical systems, and Koopman operator theory in particular, can be useful for problems that have historically made use of optimization theory.
翻译:Koopman 模式分解尽管目标相似,但两种方法大多由不同的科学界使用,并且以不同的数学语言制定。我们一起研究这两种方法,并表明,在数据某种(合理)条件下, Exor 组件分析给出的理论分解是Koopman 模式分解所给出的\ textit{same}。这提供了将高维数据集分解成低维模式的两种流行方法,即将高维数据集分解成能够捕捉最相关特征和/或动态的低维模式。尽管其目标相似,但这两种方法大多由不同的科学界使用,并以不同的数学语言制定。我们一起研究这两种方法,并表明,在数据分析的某种(合理)条件下, 高压组件分析给出的理论分解为Koopman 模式拆解和高压组件拆解提供了新的算方法。这为两个社区提供了一种“连接”方法,可以更有效地进行交流。在不满足这一条件时,Koopman 模式分解模式的“连接”, 提供了一种新的理论, 也就是对高压系统的成功性分析的理论, 能够形成一种动态的理论,, 使高压系统在不断的系统上展示成型分析中不断形成的理论, 能够形成一个动态的理论, 成为一种动态的理论。