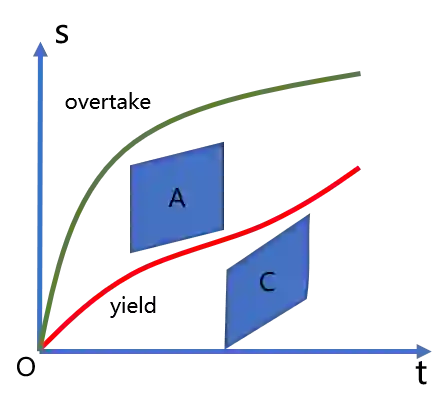
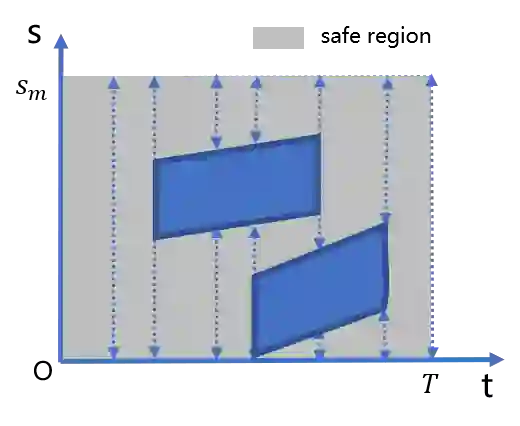
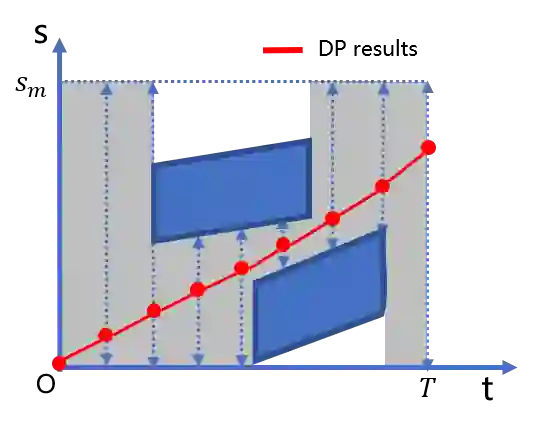
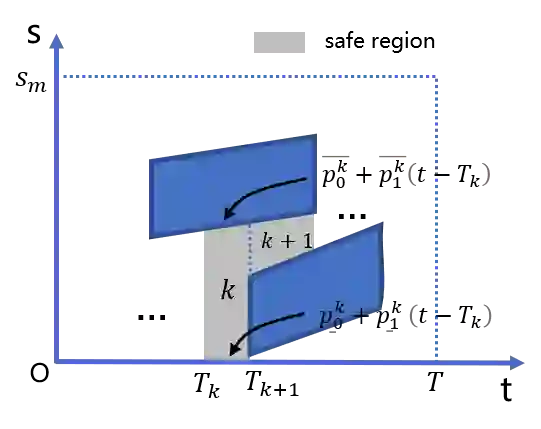
To generate safe and real-time trajectories for an autonomous vehicle in dynamic environments, path and speed decoupled planning methods are often considered. This paper studies speed planning, which mainly deals with dynamic obstacle avoidance given the planning path. The main challenges lie in the decisions in non-convex space and the trade-off between safety, comfort and efficiency performances. This work uses dynamic programming to search heuristic waypoints on the S-T graph and to construct convex feasible spaces. Further, a piecewise Bezier polynomials optimization approach with trapezoidal corridors is presented, which theoretically guarantees the safety and optimality of the trajectory. The simulations verify the effectiveness of the proposed approach.
翻译:经常考虑在动态环境、道路和速度脱钩的规划方法中为自主车辆创造安全和实时的轨迹。本文研究速度规划,主要处理在规划过程中避免动态障碍的问题。主要挑战在于非阴道空间的决定以及安全、舒适和效率性能之间的权衡。这项工作利用动态编程来搜索S-T图上的超常路径点,并建造可操作的空间。此外,还介绍了一个带捕捉性亚化物走廊的碎片化贝泽多尼西亚优化方法,从理论上保证轨迹的安全和最佳性。模拟核查了拟议方法的有效性。