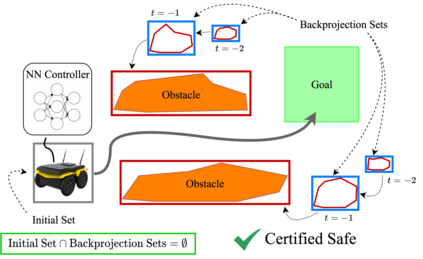
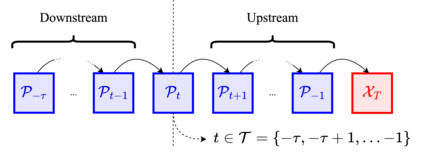
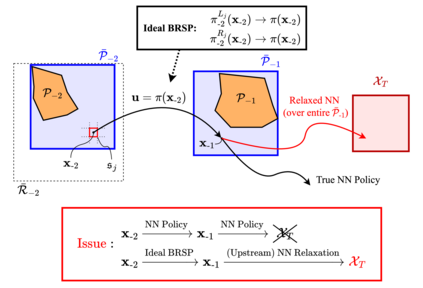
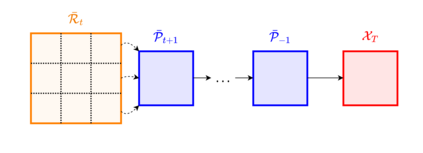
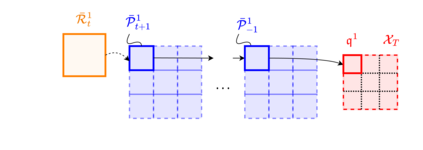
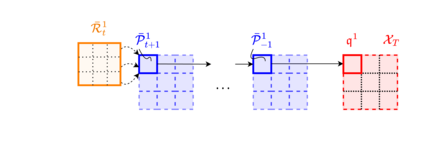
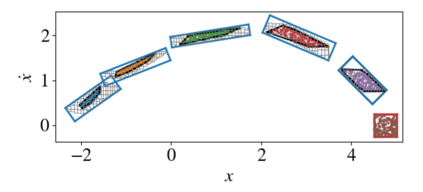
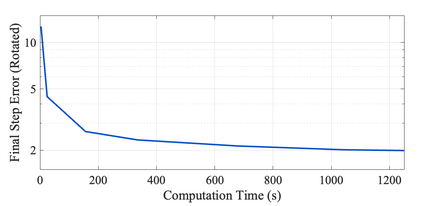
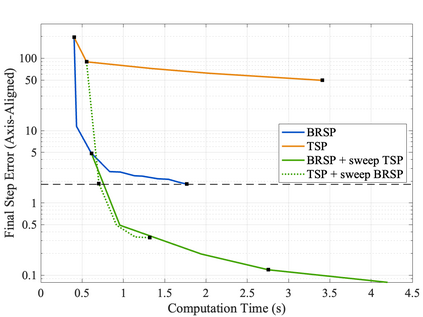
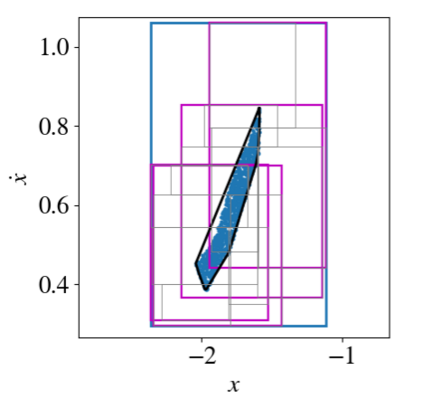
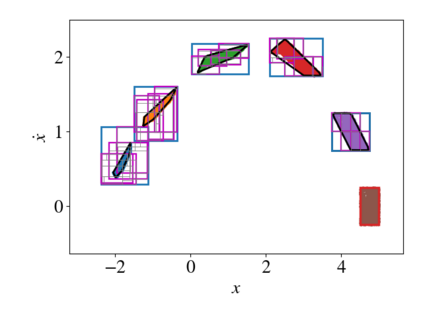
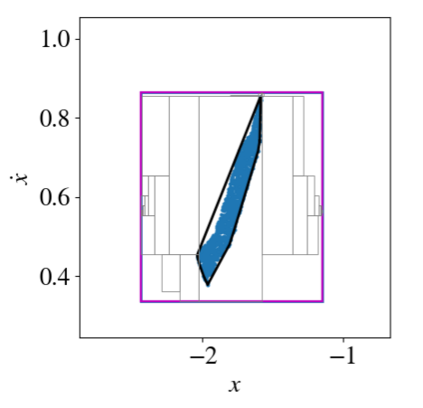
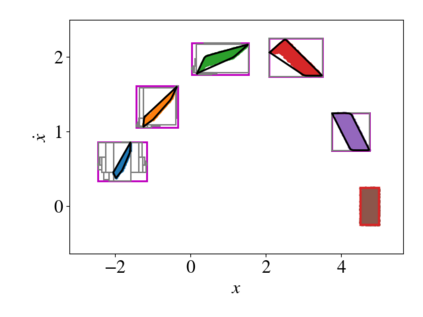
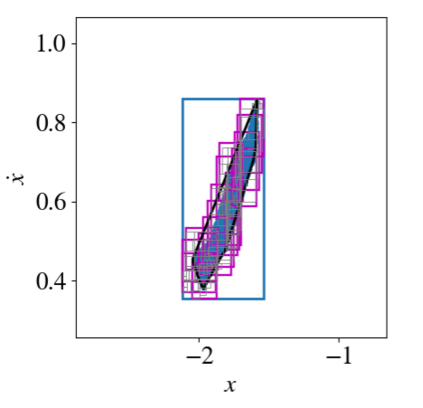
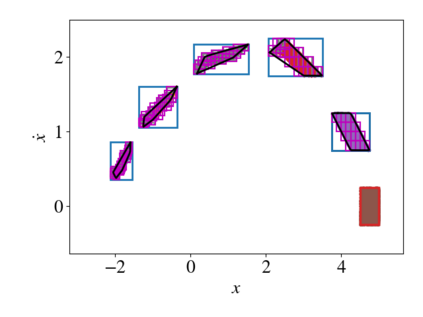
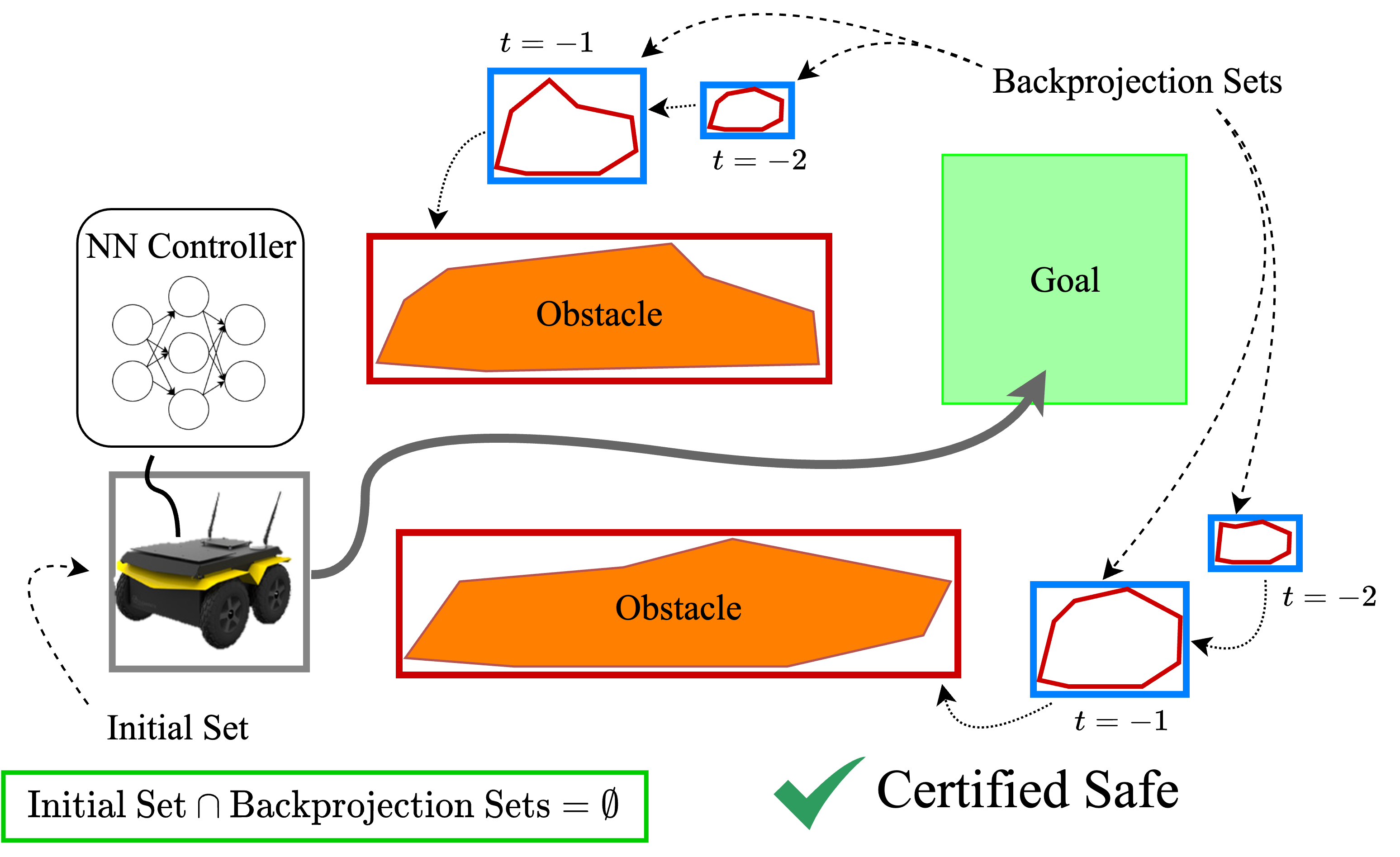
As neural networks become more integrated into the systems that we depend on for transportation, medicine, and security, it becomes increasingly important that we develop methods to analyze their behavior to ensure that they are safe to use within these contexts. The methods used in this paper seek to certify safety for closed-loop systems with neural network controllers, i.e., neural feedback loops, using backward reachability analysis. Namely, we calculate backprojection (BP) set over-approximations (BPOAs), i.e., sets of states that lead to a given target set that bounds dangerous regions of the state space. The system's safety can then be certified by checking its current state against the BPOAs. While over-approximating BPs is significantly faster than calculating exact BP sets, solving the relaxed problem leads to conservativeness. To combat conservativeness, partitioning strategies can be used to split the problem into a set of sub-problems, each less conservative than the unpartitioned problem. We introduce a hybrid partitioning method that uses both target set partitioning (TSP) and backreachable set partitioning (BRSP) to overcome a lower bound on estimation error that is present when using BRSP. Numerical results demonstrate a near order-of-magnitude reduction in estimation error compared to BRSP or TSP given the same computation time.
翻译:随着神经网络日益融入我们依赖的运输、医药和安全系统,我们越来越有必要制定分析其行为的方法,以确保这些系统在这些情况下安全使用。本文件使用的方法是,通过神经网络控制器,即神经回馈环,利用向后可达性分析,对神经网络控制器的闭路系统的安全性进行认证,即神经回路回路。也就是说,我们计算反射(BPPA)设置的超对称(BPOAs),即导致设定特定目标的一组国家,将国家空间的危险区域捆绑起来。然后,系统的安全可以通过对照BPOA检查其当前状态来证明。虽然超过接近的BPSPs比计算准确的 BP 组合要快得多,但解决宽松的问题会导致保守性。为了克服保守性,可以使用分治战略将问题分成一组子问题,每个小问题都比非分立的问题保守。我们引入一种混合分隔方法,既使用设定目标的分治(TSP),也用当前定下的时间间隔(TSP),又用BSSP下调的折算结果来显示BSP的缩后偏差。