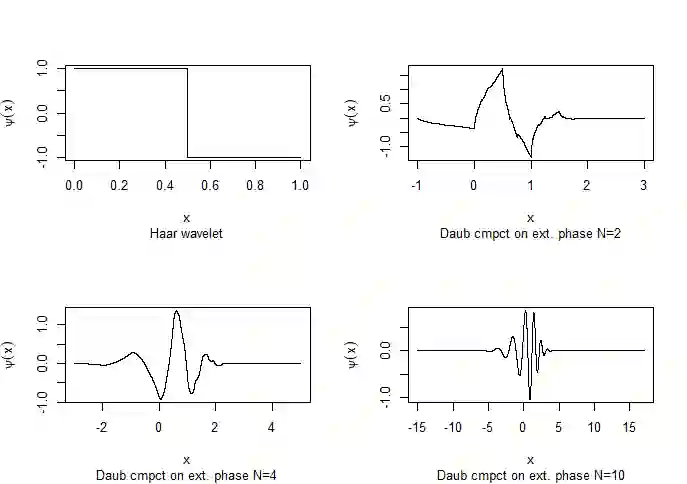
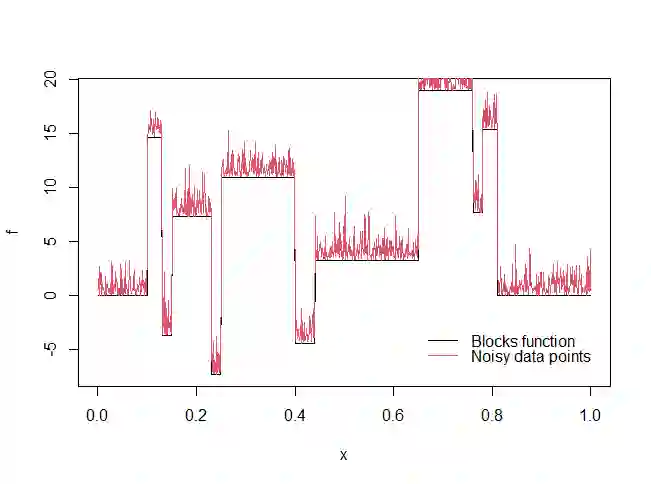
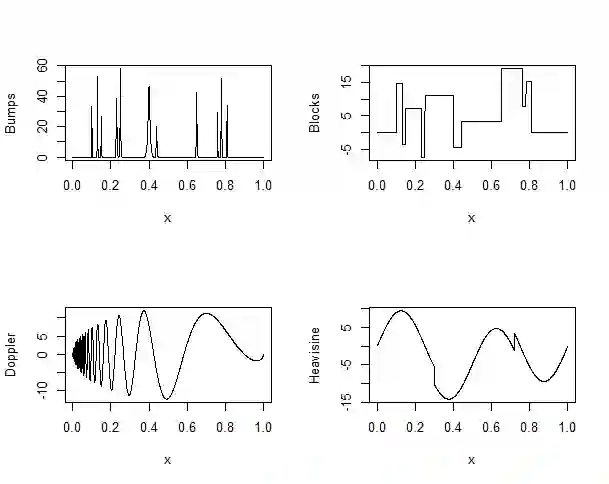
Wavelet shrinkage estimators are widely applied in several fields of science for denoising data in wavelet domain by reducing the magnitudes of empirical coefficients. In nonparametric regression problem, most of the shrinkage rules are derived from models composed by an unknown function with additive gaussian noise. Although gaussian noise assumption is reasonable in several real data analysis, mainly for large sample sizes, it is not general. Contaminated data with positive noise can occur in practice and nonparametric regression models with positive noise bring challenges in wavelet shrinkage point of view. This work develops bayesian shrinkage rules to estimate wavelet coefficients from a nonparametric regression framework with additive and strictly positive noise under exponential and lognormal distributions. Computational aspects are discussed and simulation studies to analyse the performances of the proposed shrinkage rules and compare them with standard techniques are done. An application in winning times Boston Marathon dataset is also provided.
翻译:在非参数回归问题中,大多数缩水规则来自由未知功能组成的模型,这些模型含有加添加的粗野噪音。虽然在几个真实的数据分析中,Goussian噪声假设是合理的,主要针对大样本大小,但并不普遍。在实际中,有积极噪音的受污染数据会发生,而有积极噪音的非参数回归模型会给波浪缩水点带来挑战。这项工作开发了海湾缩水规则,用非参数回归框架估算波浪系数,在指数和逻辑异常分布下,采用添加和严格肯定的噪音。讨论了计算问题,并进行了模拟研究,以分析拟议的缩水规则的性能,并将之与标准技术进行比较。还提供了波士顿马拉松数据集赢得时间的应用。