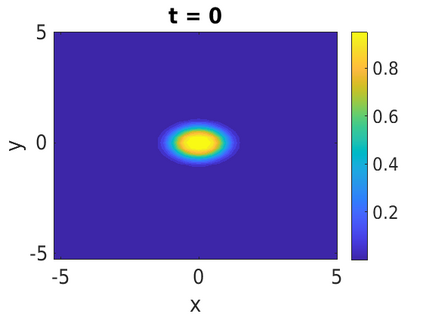
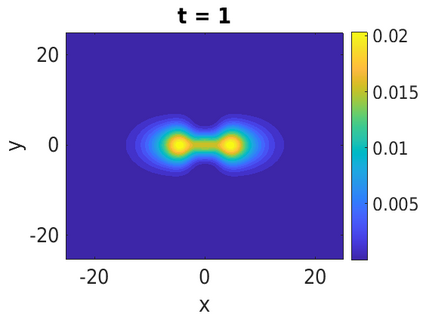
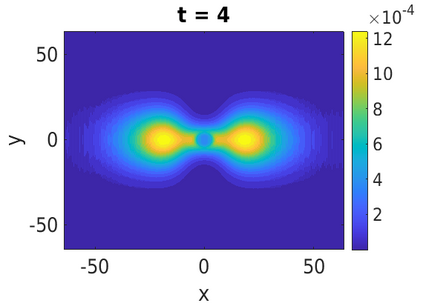
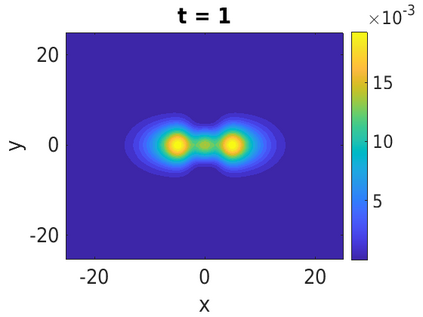
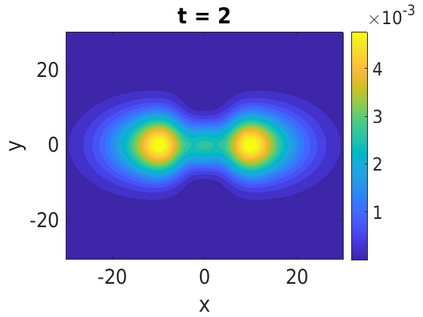
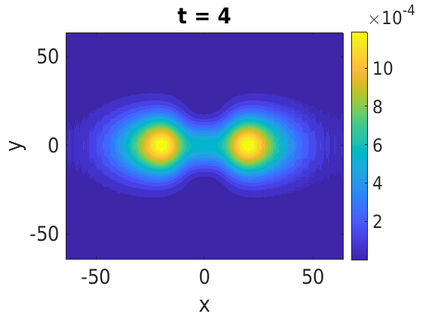
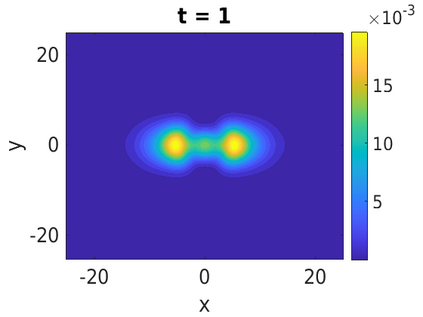
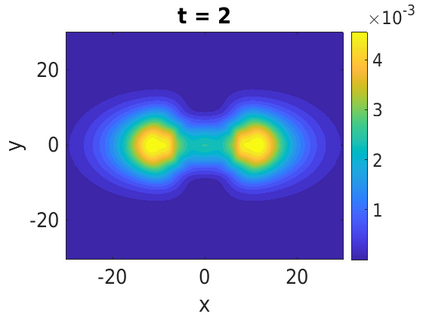
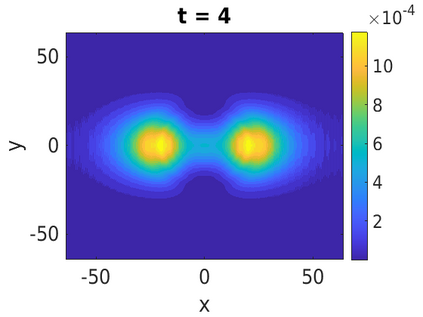
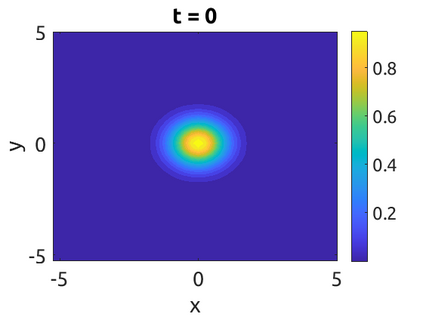
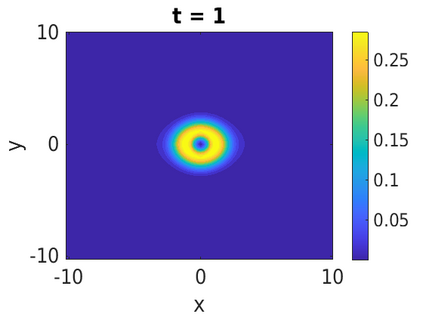
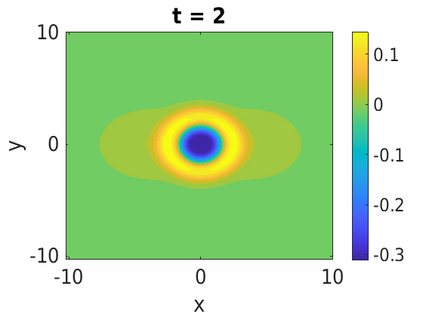
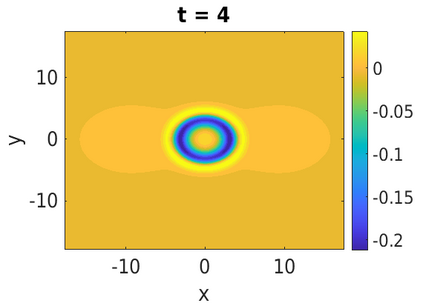
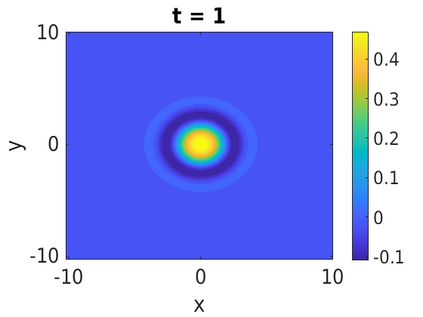
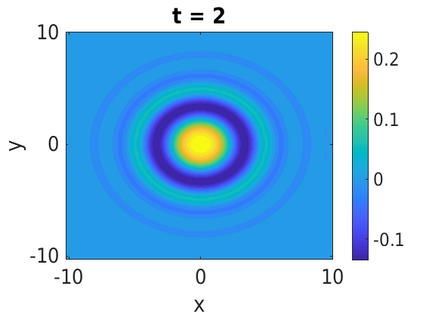
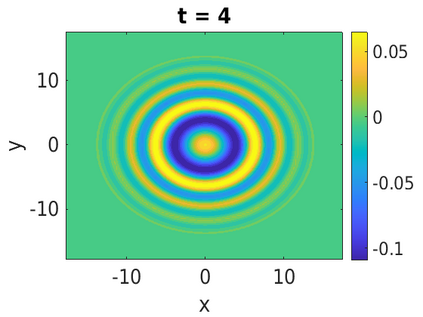
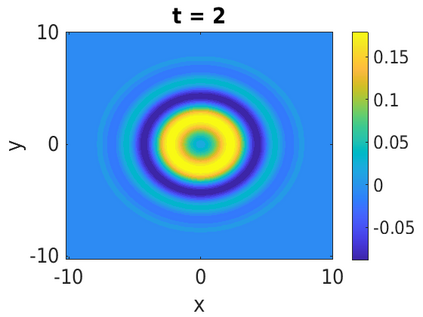
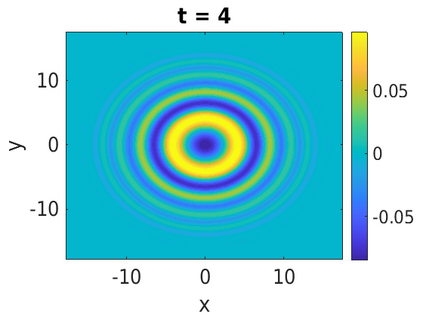
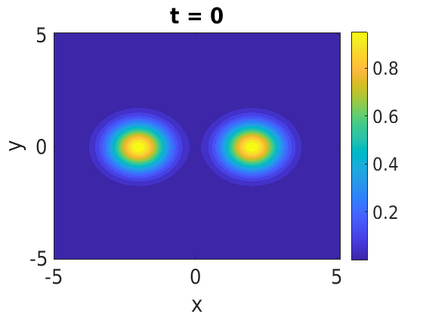
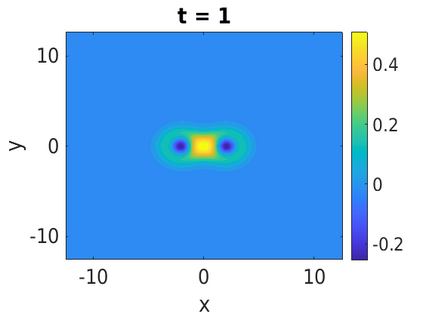
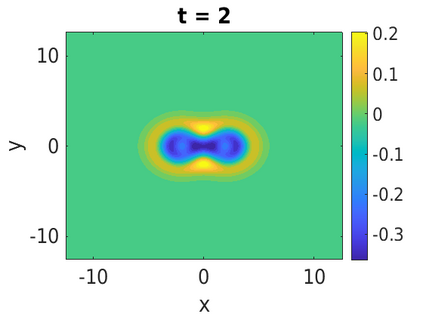
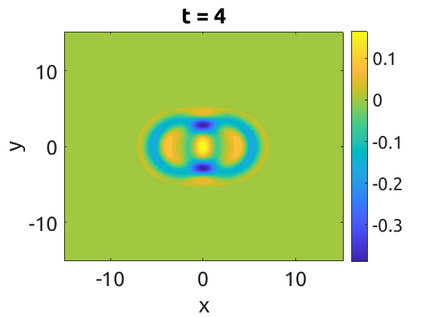
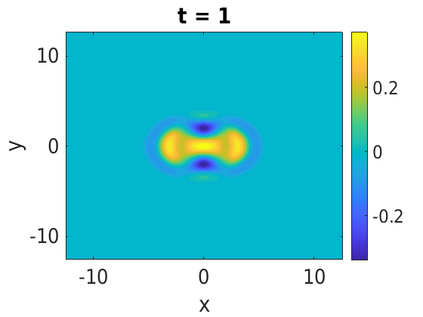
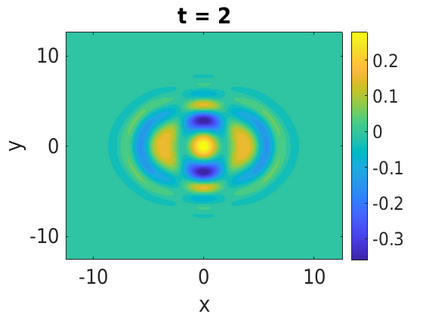
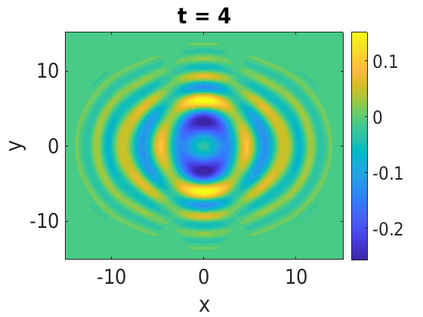
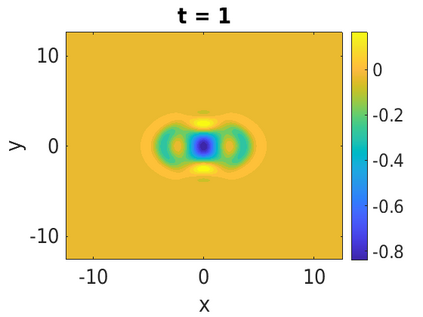
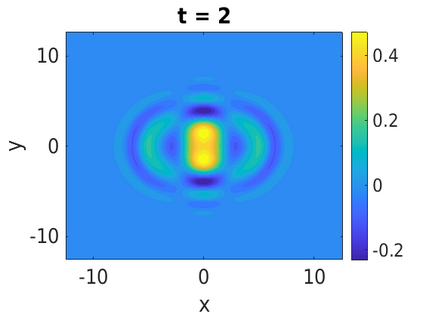
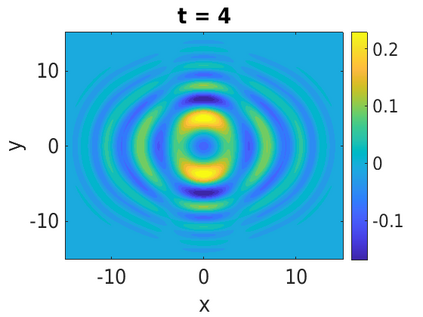
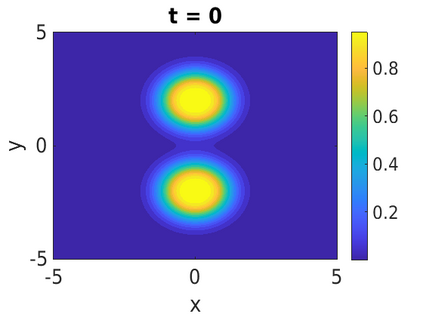
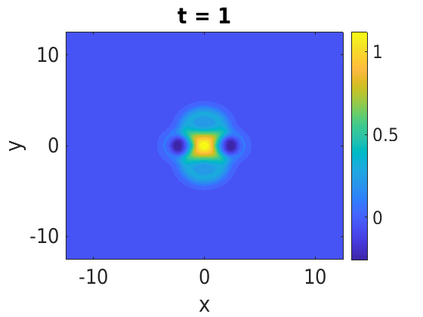
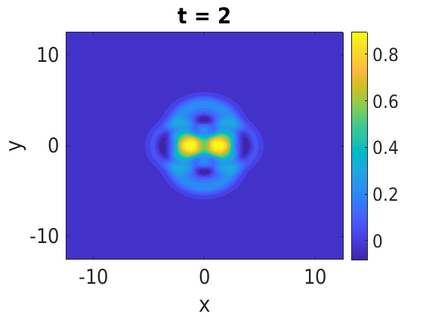
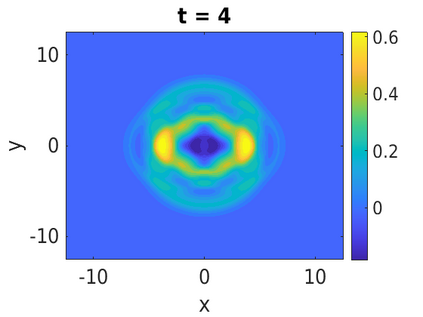
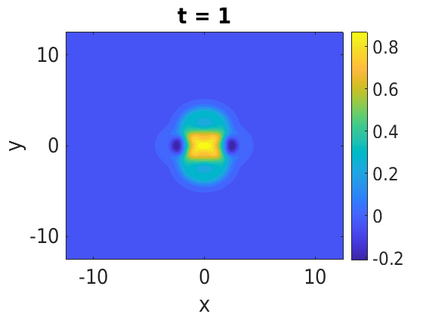
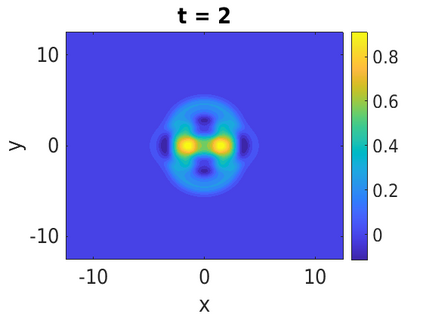
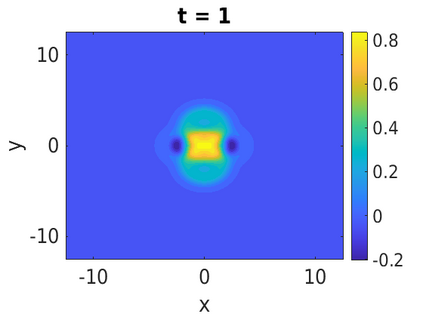
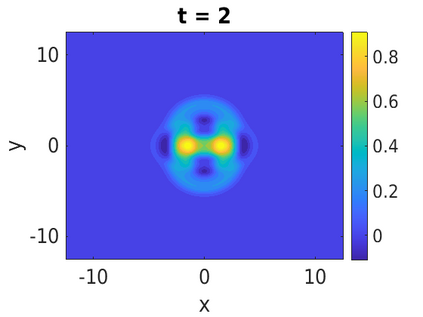
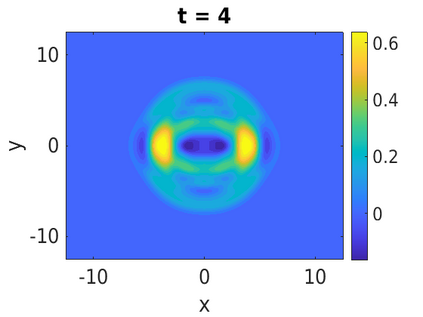
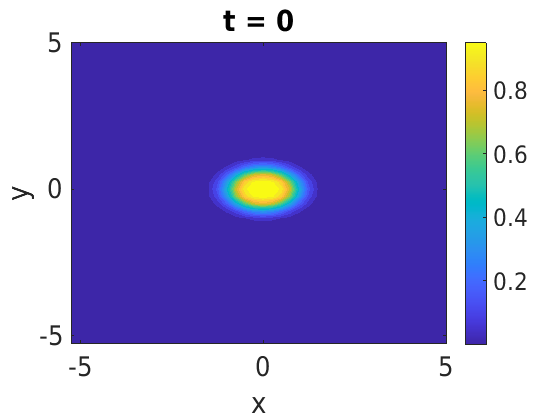
In this paper, we develop a framework to construct energy-preserving methods for multi-components Hamiltonian systems, combining the exponential integrator and the partitioned averaged vector field method. This leads to numerical schemes with both advantages of long-time stability and excellent behavior for highly oscillatory or stiff problems. Compared to the existing energy-preserving exponential integrators (EP-EI) in practical implementation, our proposed methods are much efficient which can at least be computed by subsystem instead of handling a nonlinear coupling system at a time. Moreover, for most cases, such as the Klein-Gordon-Schr\"{o}dinger equations and the Klein-Gordon-Zakharov equations considered in this paper, the computational cost can be further reduced. Specifically, one part of the derived schemes is totally explicit, and the other is linearly implicit. In addition, we present rigorous proof of conserving the original energy of Hamiltonian systems, in which an alternative technique is utilized so that no additional assumptions are required, in contrast to the proof strategies used for the existing EP-EI. Numerical experiments are provided to demonstrate the significant advantages in accuracy, computational efficiency, and the ability to capture highly oscillatory solutions.
翻译:在本文中,我们为多构件汉密尔顿系统制定了一个构建节能方法的框架,将指数集成器和平均分布式矢量场方法结合起来,从而形成具有长期稳定性优势和高度振动性或严重问题优异行为优异性的数字方法。与现有的节能指数集成器(EP-EI)实际实施相比,我们提出的方法非常高效,至少可以由子系统而不是同时处理非线性连接系统来计算。此外,对于大多数情况,例如克莱因-哥尔登-施尔-{欧丁格方程式和本文中考虑的克莱因-哥尔登-扎卡罗夫方程式等式,计算成本可以进一步降低。具体地说,与现有的节能指数集成器(EP-E-E-EI)相比,一部分是完全明确的,另一部分是线性隐含的。此外,我们提出了保护汉密尔顿系统原始能量的有力证据,其中使用了一种替代技术,因此不需要额外的假设,与现有的EP-EP-E-E-E-E-E-E-Charkoval 的精确度计算能力模型相比,提供了重大精确度和高精确性计算能力的优势。