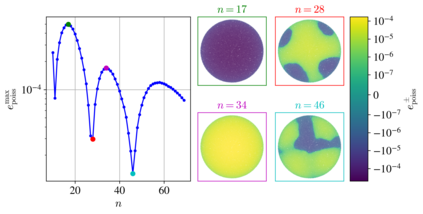
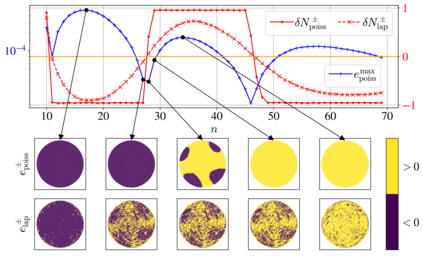
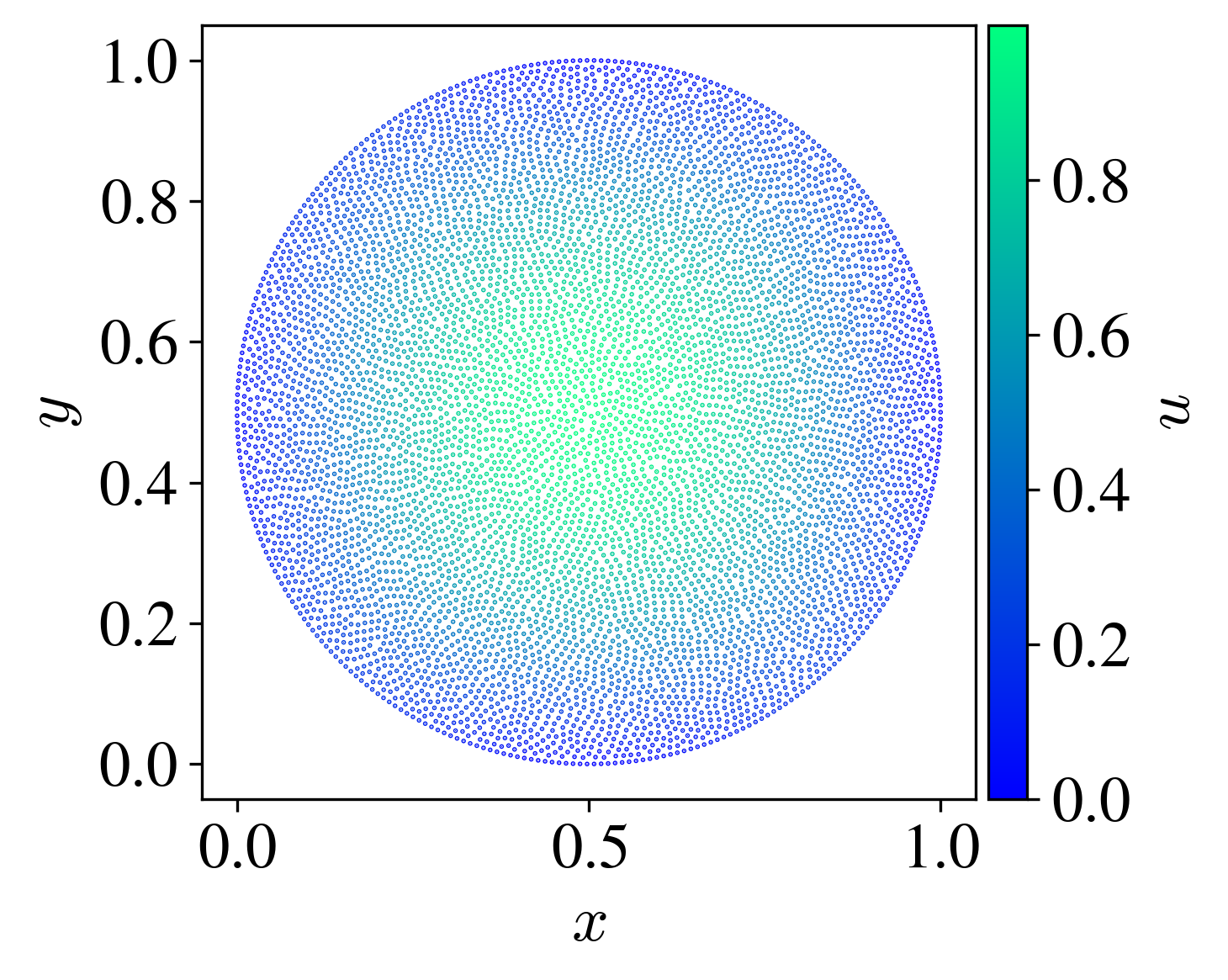
When solving partial differential equations on scattered nodes using the Radial Basis Function generated Finite Difference (RBF-FD) method, one of the parameters that must be chosen is the stencil size. Focusing on Polyharmonic Spline RBFs with monomial augmentation, we observe that it affects the approximation accuracy in a particularly interesting way - the solution error oscillates under increasing stencil size. We find that we can connect this behaviour with the spatial dependence of the signed approximation error. Based on this observation we are then able to introduce a numerical quantity that indicates whether a given stencil size is locally optimal.
翻译:在使用RBF-FD方法在扩散节点上求解偏微分方程时,必须选择模板大小之一。重点研究了具有单项式增强的多次谐波样条RBF,发现它以一种特别有趣的方式影响逼近精度-在增加模板大小下,解决方案误差会振荡。我们发现,我们可以将这种行为与带符号逼近误差的空间依赖性联系起来。基于这个观察结果,我们能够引入一种数字量,指示一个给定的模板大小是否在局部上是最优的。