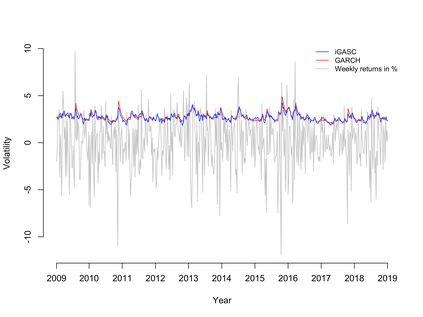
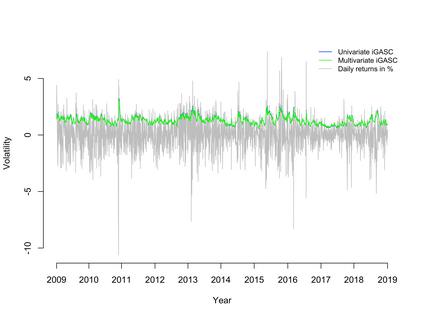
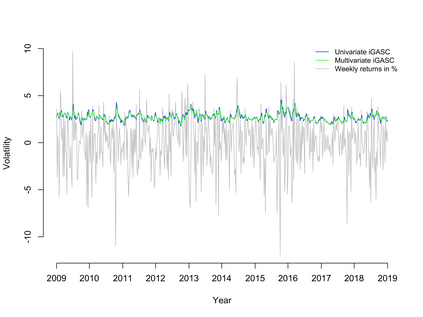
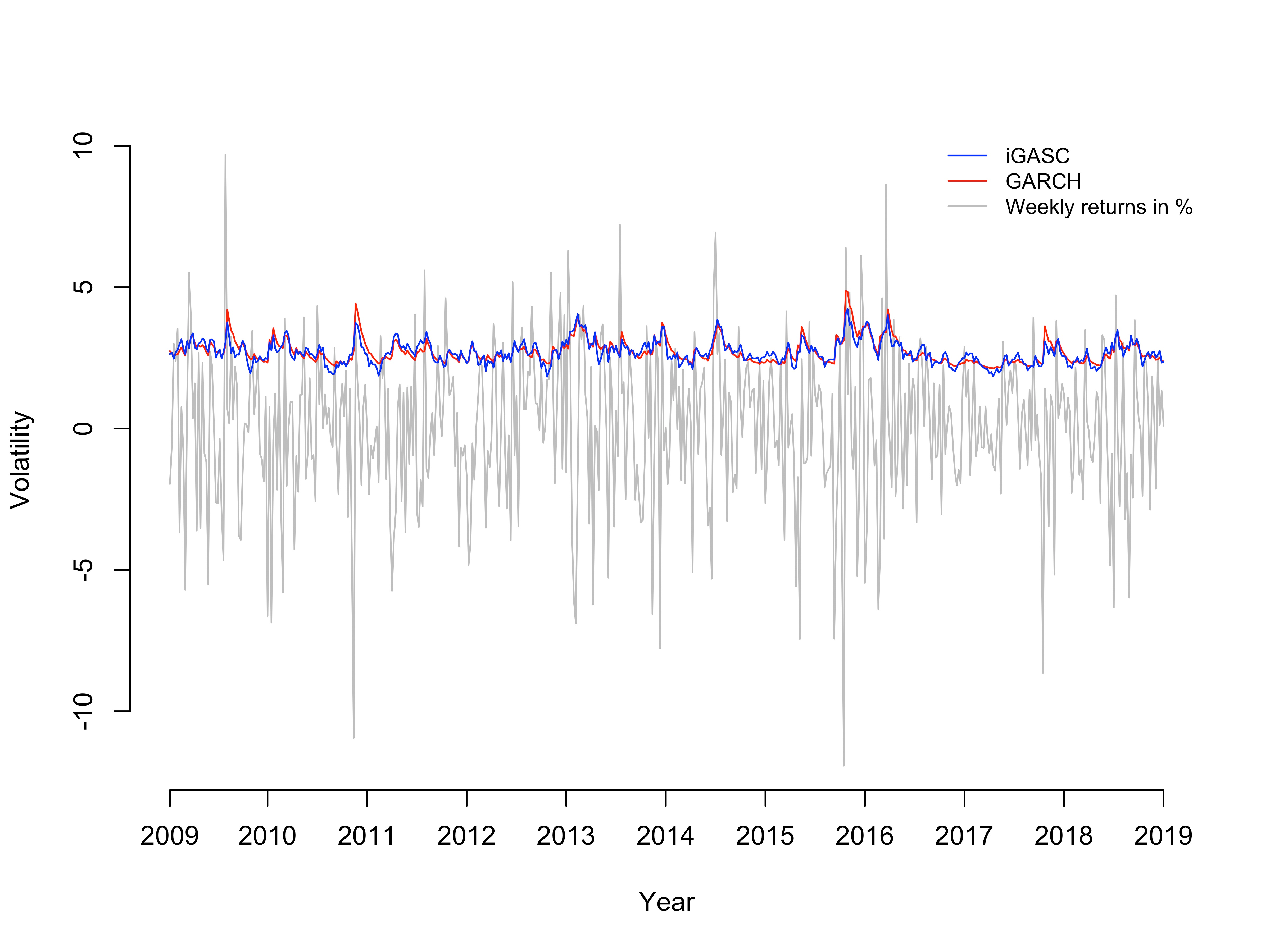
This paper introduces a new class of observation driven dynamic models. The time evolving parameters are driven by innovations of copula form. The resulting models can be made strictly stationary and the innovation term is typically chosen to be Gaussian. The innovations are formed by applying a copula approach for the conditional score function which has close connections the existing literature on GAS models. This new method provides a unified framework for observation-driven models allowing the likelihood to be explicitly computed using the prediction decomposition. The approach may be used for multiple lag structures and for multivariate models. Strict stationarity can be easily imposed upon the models making the invariant properties simple to ascertain. This property also has advantages for specifying the initial conditions needed for maximum likelihood estimation. One step and multi-period forecasting is straight-forward and the forecasting density is either in closed form or a simple mixture over a univariate component. The approach is very general and the illustrations focus on volatility models and duration models. We illustrate the performance of the modelling approach for both univariate and multivariate volatility models.
翻译:本文引入了一个新的观测驱动动态模型类别。 时间变化参数是由千叶形形式的创新驱动的。 由此产生的模型可以严格固定, 创新术语通常被选择为高斯。 这些创新是通过对有条件的评分函数采用千叶式方法形成的, 有条件的评分函数与关于GAS模型的现有文献有着密切的联系。 这个新方法为观测驱动模型提供了一个统一框架, 使得有可能使用预测分解来明确计算。 这种方法可用于多个滞后结构和多变量模型。 严格的定位性可以很容易地强加给使变量属性简单化的模型。 这个属性还有利于确定最大可能性估算所需的初始条件。 一步和多期预报是直向的, 预测密度要么是封闭式的, 要么是单向式组件的简单混合物。 这种方法非常笼统, 插图侧重于波动模型和持续期模型。 我们说明了单向和多变量波动模型的模拟方法的绩效。