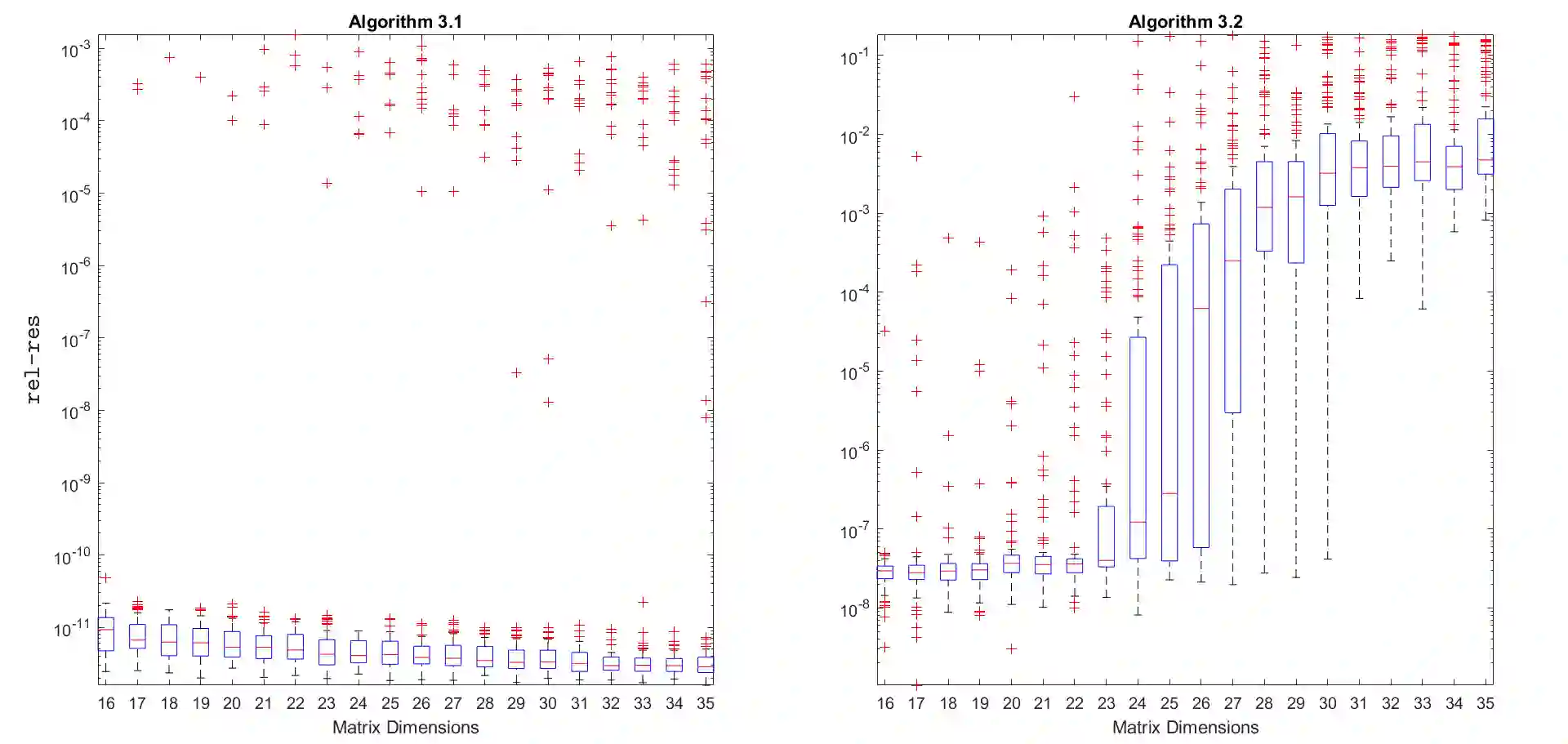
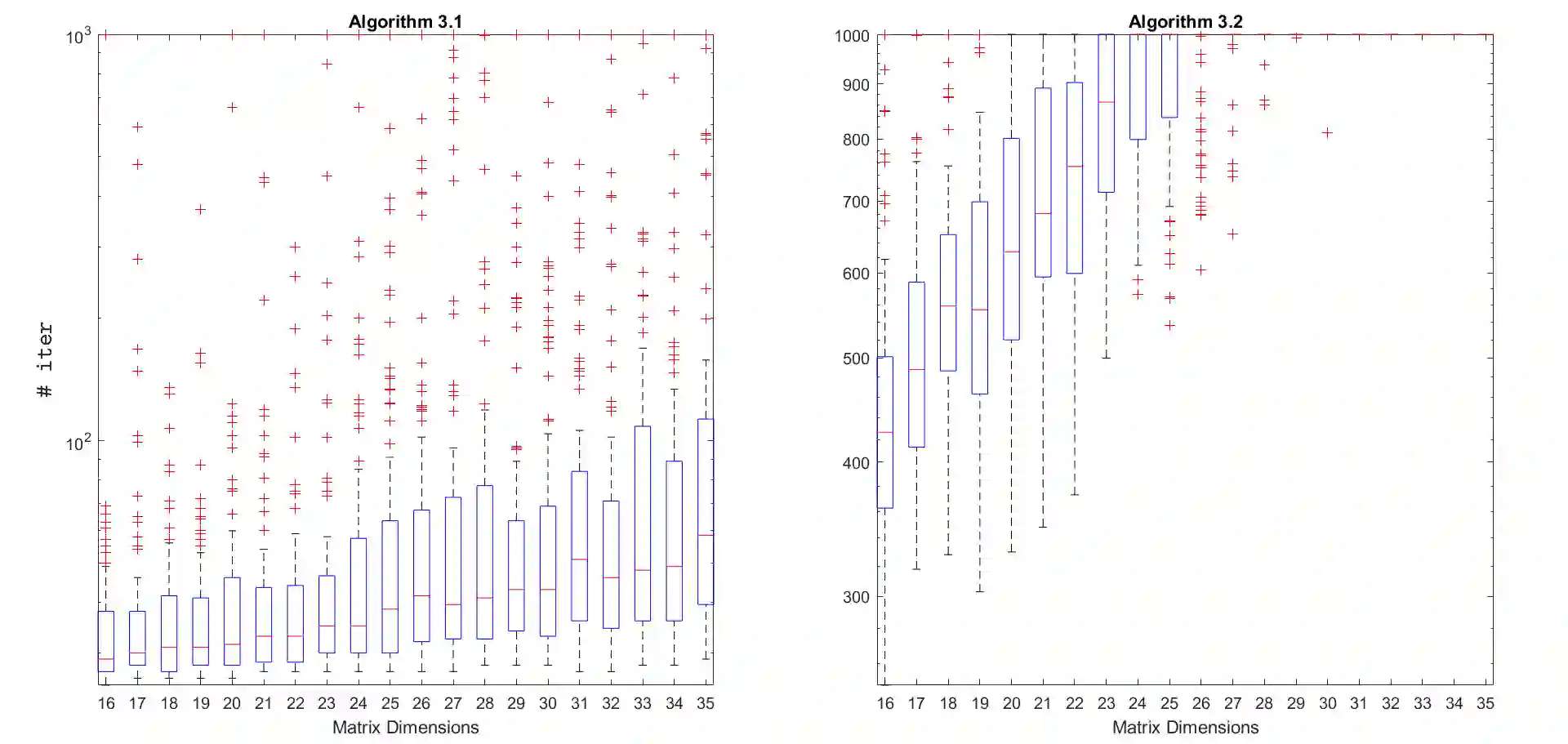
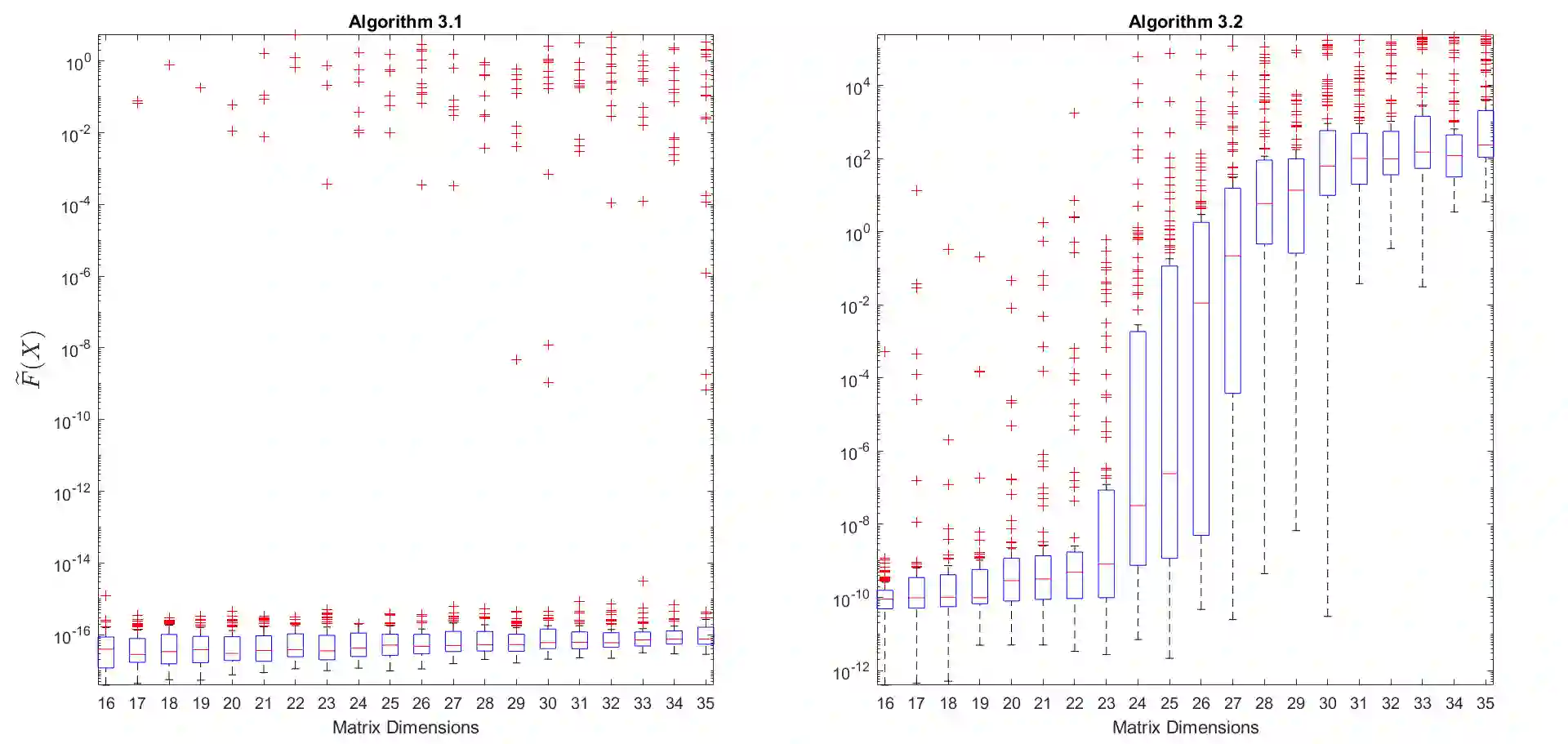
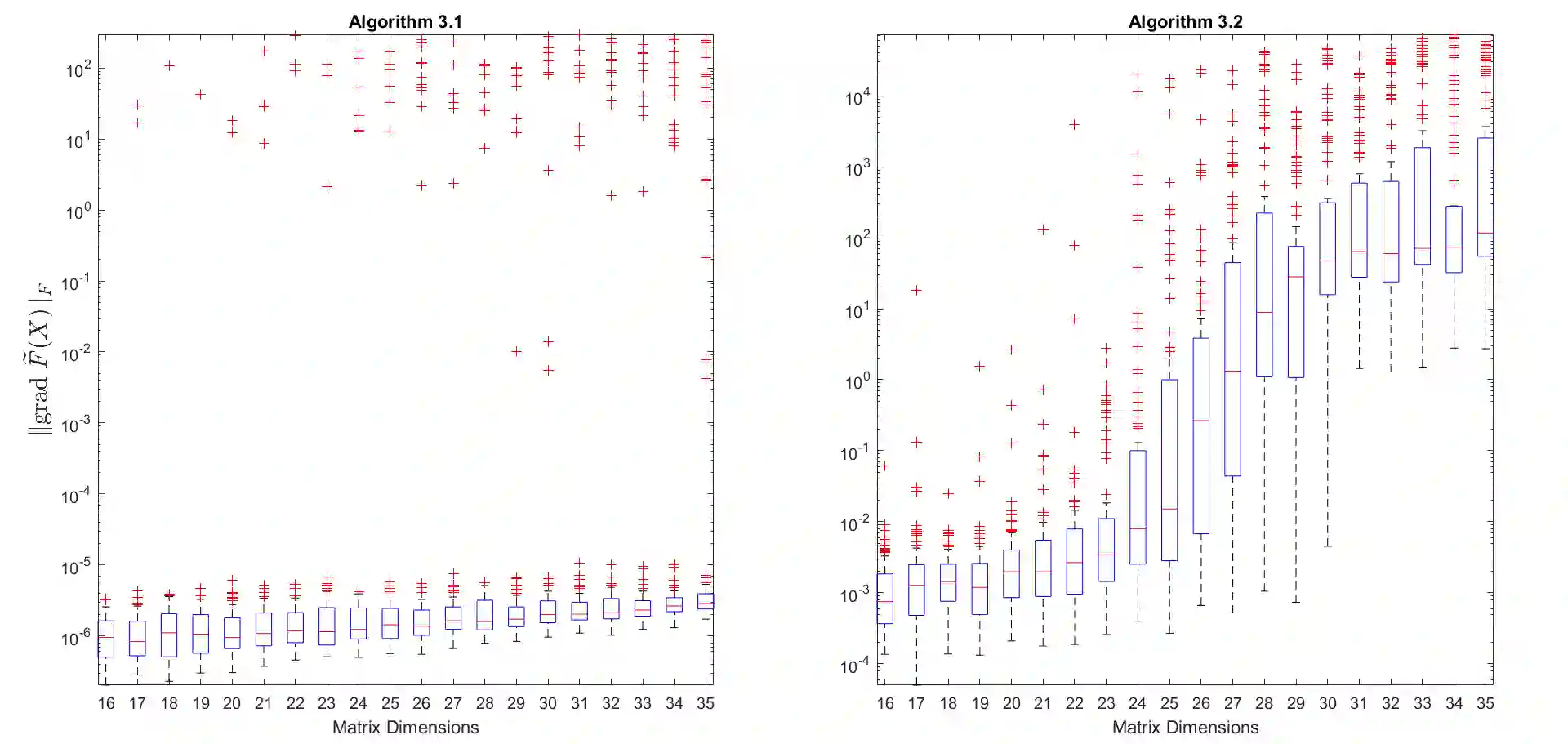
We propose three iterative methods for solving the Moser-Veselov equation, which arises in the discretization of the Euler-Arnold differential equations governing the motion of a generalized rigid body. We start by formulating the problem as an optimization problem with orthogonal constraints and proving that the objective function is convex. Then, using techniques from optimization on Riemannian manifolds, the three feasible algorithms are designed. The first one splits the orthogonal constraints using the Bregman method, whereas the other two methods are of the steepest-descent type. The second method uses the Cayley-transform to preserve the constraints and a Barzilai-Borwein step size, while the third one involves geodesics, with the step size computed by Armijo's rule. Finally, a set of numerical experiments are carried out to compare the performance of the proposed algorithms, suggesting that the first algorithm has the best performance in terms of accuracy and number of iterations. An essential advantage of these iterative methods is that they work even when the conditions for applicability of the direct methods available in the literature are not satisfied.
翻译:我们提出三种迭代方法来解决摩瑟-维斯洛夫等式,这三种方法产生于关于通用僵硬体运动的欧勒-阿诺尔德差分方程式的分解。我们首先将问题作为正方形限制的优化问题提出,并证明客观功能是二次曲线。然后,利用在里伊曼尼方形上的优化技术,设计出三种可行的算法。第一种是使用布雷格曼法分割正方形限制,而其他两种方法则是最陡峭的白种。第二种是使用凯利变形法来保持限制和巴齐莱-波尔文级大小,而第三个方法则涉及大地测量学,而阿尔米乔规则则计算了分级大小。最后,进行了一系列数字实验,以比较拟议算法的性能,表明第一个算法在准确性和迭代数方面表现最佳。这些迭代法的一个基本优点是,即使在现有直接方法的适用性条件不令人满意的情况下,它们仍然起作用。