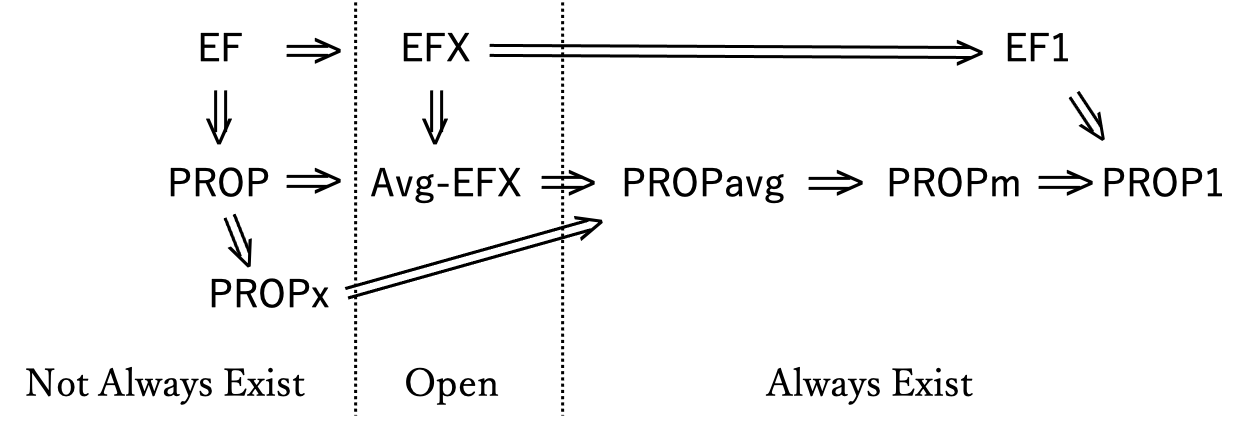
We study the problem of fairly allocating a set of indivisible goods to multiple agents and focus on the proportionality, which is one of the classical fairness notions. Since proportional allocations do not always exist when goods are indivisible, approximate concepts of proportionality have been considered in the previous work. Among them, proportionality up to the maximin good (PROPm) has been the best approximate notion of proportionality that can be achieved for all instances. In this paper, we introduce the notion of proportionality up to the least valued good on average (PROPavg), which is a stronger notion than PROPm, and show that a PROPavg allocation always exists. Our results establish PROPavg as a notable non-trivial fairness notion that can be achieved for all instances. Our proof is constructive, and based on a new technique that generalizes the cut-and-choose protocol.
翻译:我们研究将一组不可分割的商品公平分配给多个代理人的问题,并注重相称性,这是典型的公平概念之一;由于在货物不可分割的情况下,比例分配并不总是存在的,在以往的工作中已经考虑了近似比例性的概念;其中,到最大货物(PROPm)的相称性是在所有情况下都能达到的最佳的相称性概念;在本文件中,我们引入了平均价值最低的商品(PROPavg)的相称性概念(PROPavg),这是一个比PROPM更强的概念,并表明始终存在PROPavg的分配。我们的结果将PROPavg确立为一种在所有情况下都可以达到的显著的非三重公平性概念。我们的证据是建设性的,基于一种普遍适用割裂和裁剪议定书的新方法。