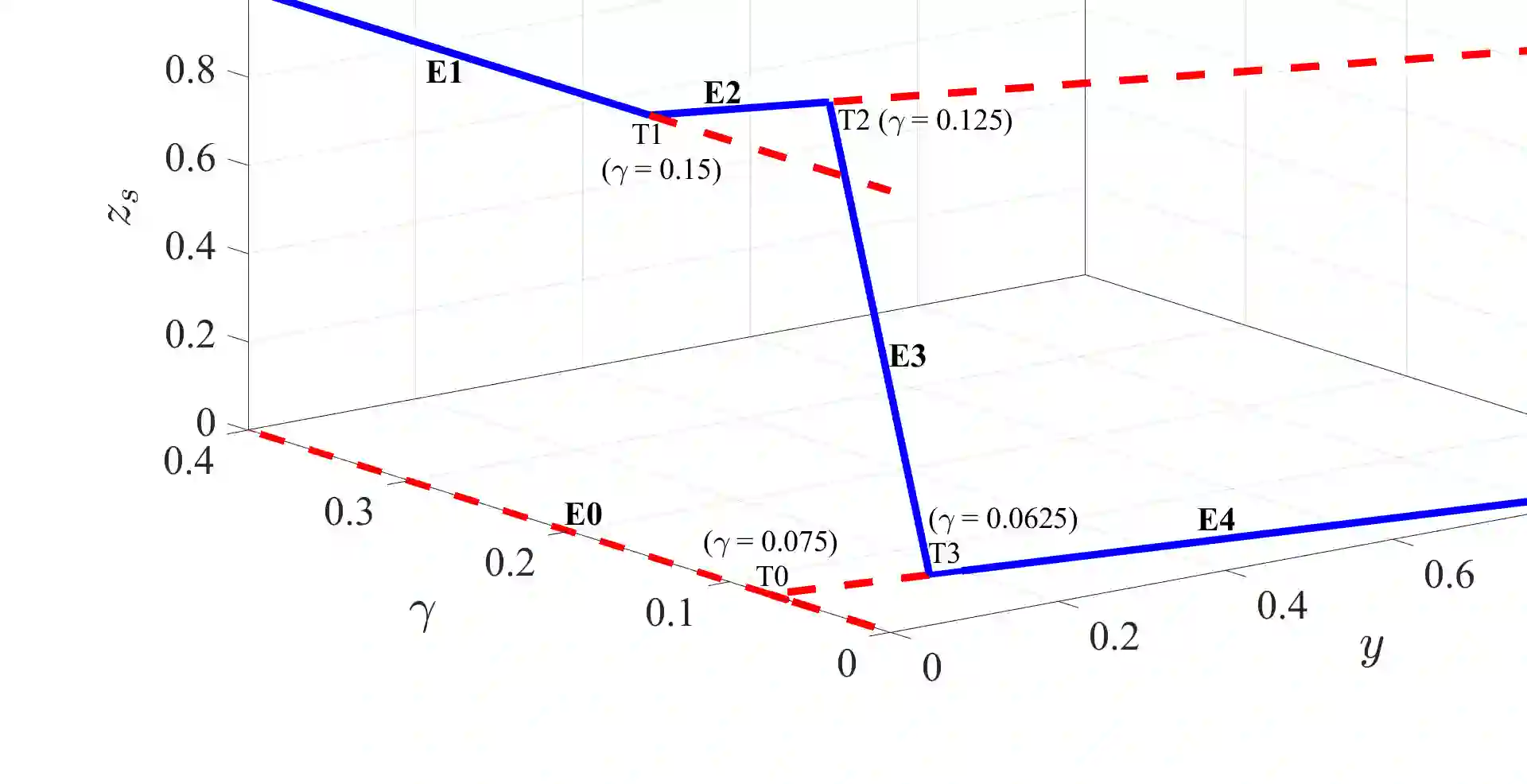
We study the interplay between epidemic dynamics and human decision making for epidemics that involve reinfection risk; in particular, the susceptible-infected-susceptible (SIS) and the susceptible-infected-recovered-infected (SIRI) epidemic models. In the proposed game-theoretic setting, individuals choose whether to adopt protection or not based on the trade-off between the cost of adopting protection and the risk of infection; the latter depends on the current prevalence of the epidemic and the fraction of individuals who adopt protection in the entire population. We define the coupled epidemic-behavioral dynamics by modeling the evolution of individual protection adoption behavior according to the replicator dynamics. For the SIS epidemic, we fully characterize the equilibria and their stability properties. We further analyze the coupled dynamics under timescale separation when individual behavior evolves faster than the epidemic, and characterize the equilibria of the resulting discontinuous hybrid dynamical system for both SIS and SIRI models. Numerical results illustrate how the coupled dynamics exhibits oscillatory behavior and convergence to sliding mode solutions under suitable parameter regimes.
翻译:我们研究流行病动态和人类对涉及再感染风险的流行病的决策之间的相互作用;特别是易感染感染和易感染后再恢复感染的流行病模式;在提议的游戏理论环境中,个人选择是否采用保护,而不是以采用保护的成本和感染风险之间的权衡取舍;后者取决于目前流行病的流行程度和在整个人口中采用保护的个人比例;我们通过根据调剂动态模拟个人保护收养行为的演变来界定同时的流行病-行为动态。对于SIS流行病,我们充分描述平衡性及其稳定性特性。我们进一步分析在个人行为发展快于该流行病的情况下,在时间尺度上分离下的混合动态,并描述由此导致的SIS和SIRI两种模式混合动力系统不连续的平衡性。数字结果说明这些动态如何在适当的参数系统下展示了血管行为和趋同于滑动模式的解决办法。