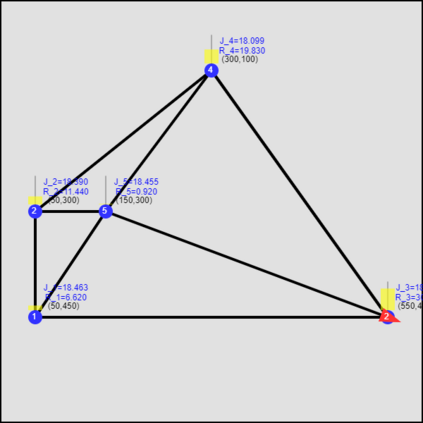
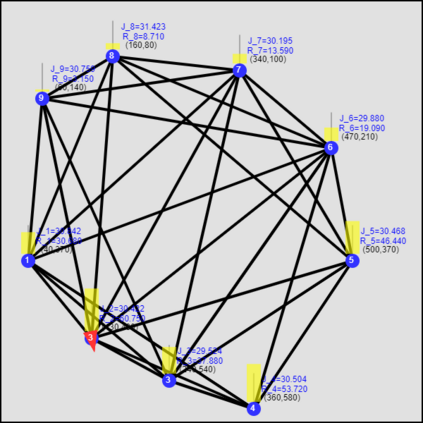
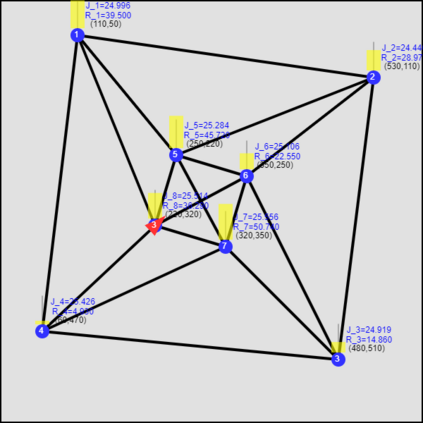
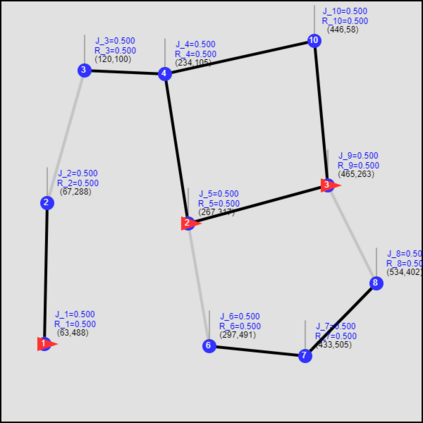
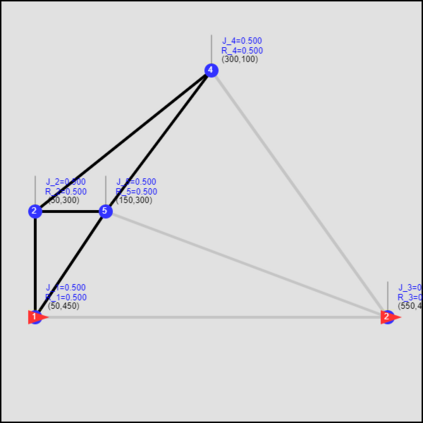
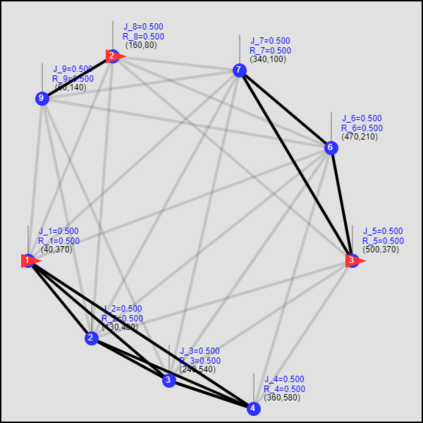
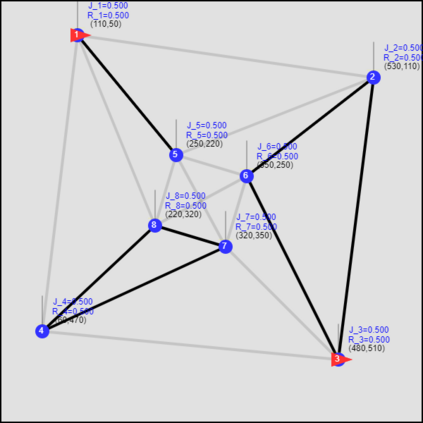
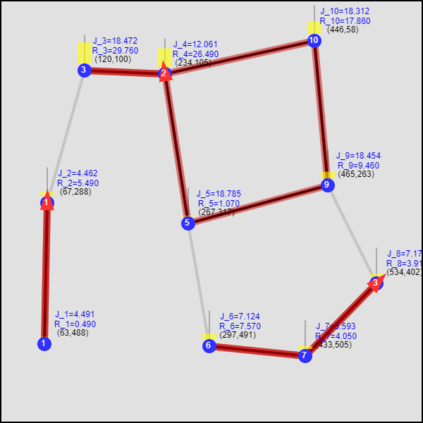
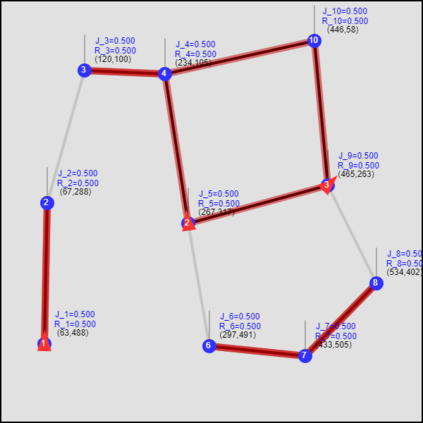
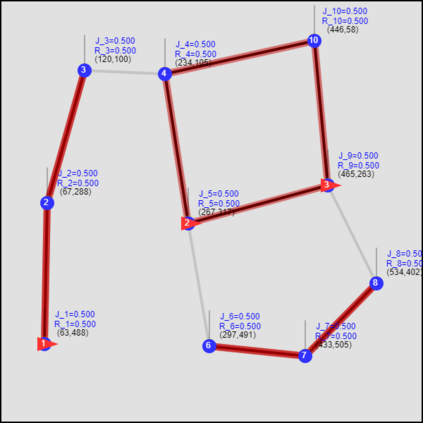
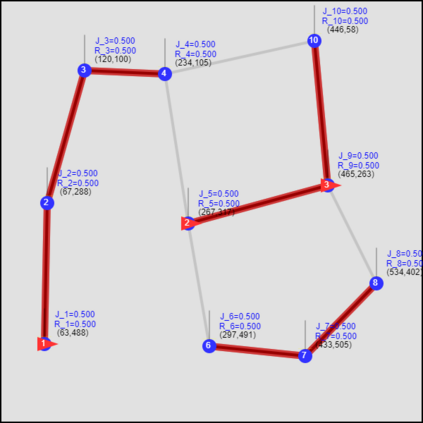
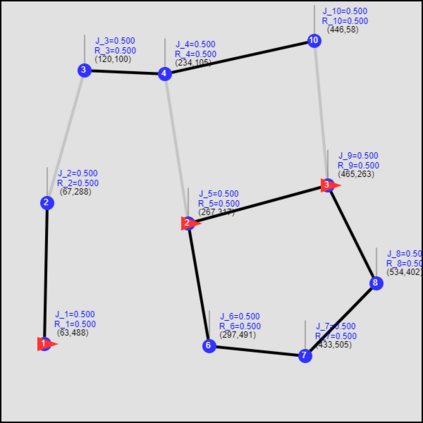
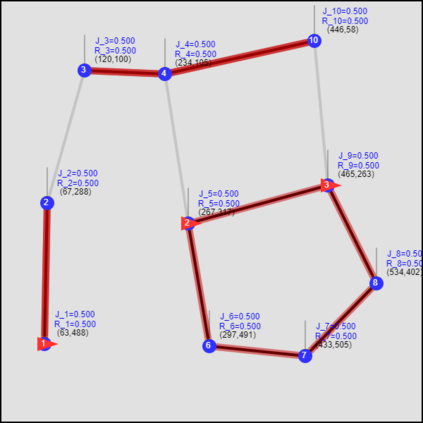
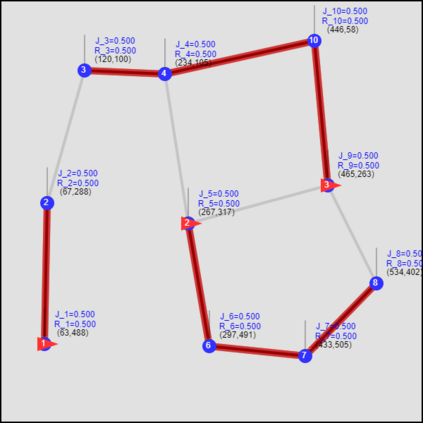
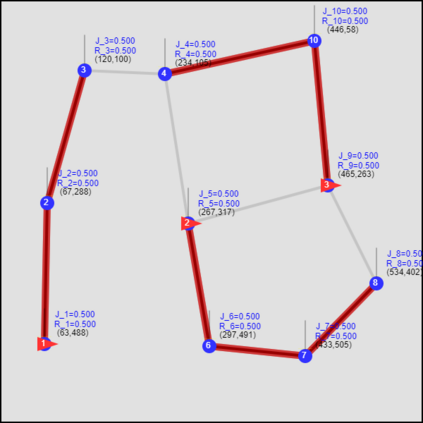
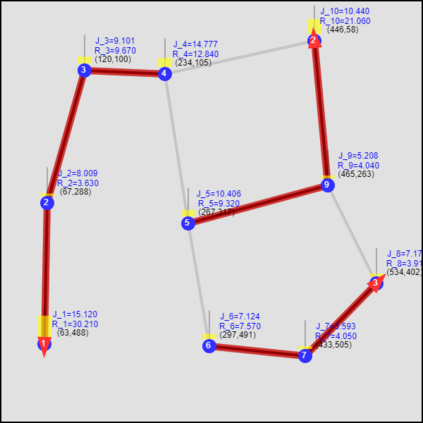
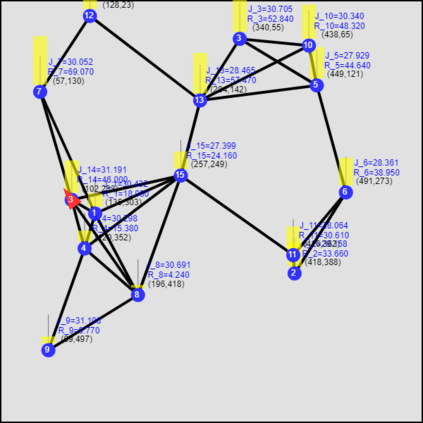
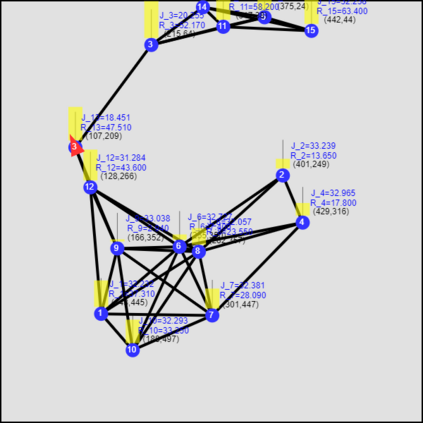
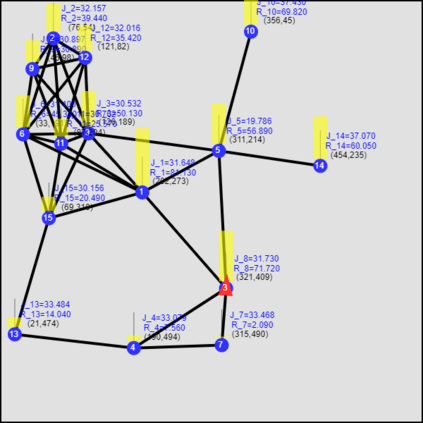
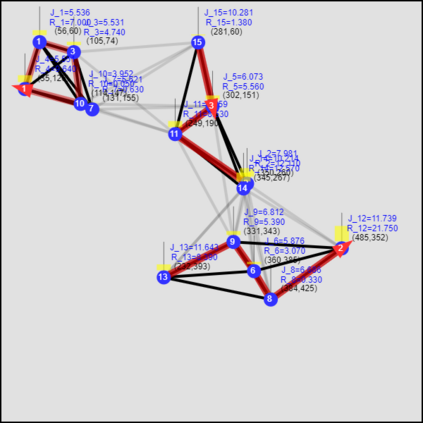
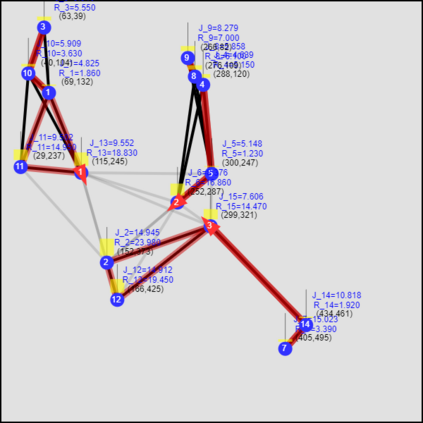
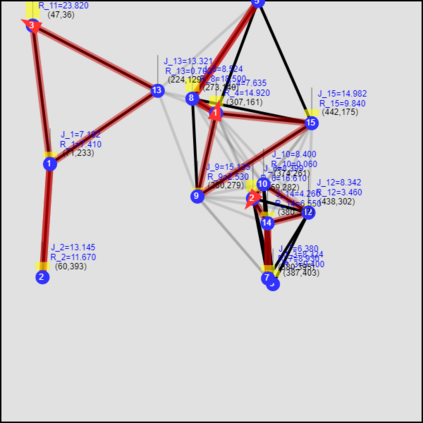
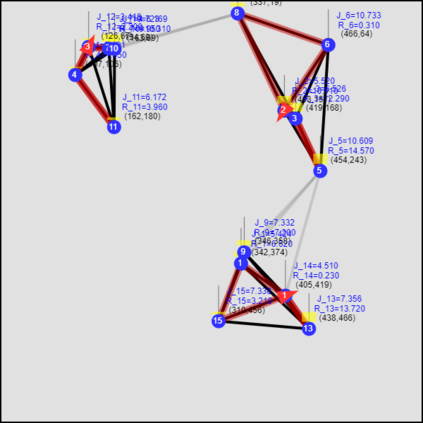
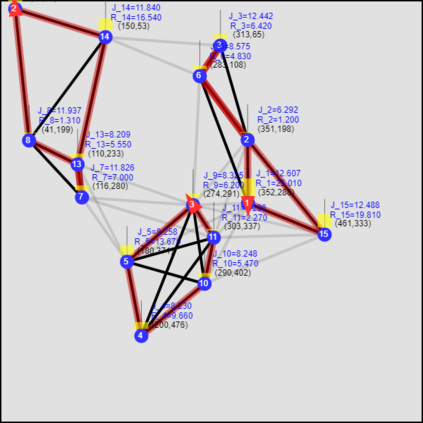
This paper considers the optimal multi-agent persistent monitoring problem defined for a team of agents on a set of nodes (targets) interconnected according to a fixed network topology. The aim is to control this team so as to minimize a measure of overall node state uncertainty evaluated over a finite time interval. A class of distributed threshold-based parametric controllers has been proposed in prior work to control agent dwell times at nodes and next-node destinations by enforcing thresholds on the respective node states. Under such a Threshold Control Policy (TCP), an on-line gradient technique was used to determine optimal threshold values. However, due to the non-convexity of the problem, this approach often leads to a poor local optima highly dependent on the initial thresholds used. To overcome this initialization challenge, we develop a computationally efficient off-line greedy technique based on the asymptotic analysis of the network system. This analysis is then used to generate a high-performing set of initial thresholds. Extensive numerical results show that such initial thresholds are almost immediately (locally) optimal or quickly lead to optimal values. In all cases, they perform significantly better than the locally optimal solutions known to date.
翻译:本文审议了一套节点(目标)根据固定的网络地形学而相互连接的一组节点(目标)上一组物剂确定的最佳多剂持久性监测问题。目的是控制这一组物,以尽量减少在一定时间间隔内评估的总体节点状态不确定性的尺度。在以前的工作中,曾建议对节点和下节点目的地控制剂停留时间进行一系列分布式临界值的参数控制器,方法是对各节点各邦执行一套高性能的阈值。在这种“临界值控制政策”(TCP)下,使用了一种在线梯度技术来确定最佳阈值。然而,由于问题不均匀,这种方法往往导致对最初阈值高度依赖的当地偏差。为了克服这一初始化挑战,我们根据对网络系统的无症状分析,开发了一种计算高效的离线性贪婪技术。然后,这种分析被用来生成一套高性的初步阈值。广泛的数字结果显示,这种初始阈值几乎立即(当地)最优化或很快导致最佳值。在所有情况中,它们比已知的最佳日期的当地解决办法要好得多。