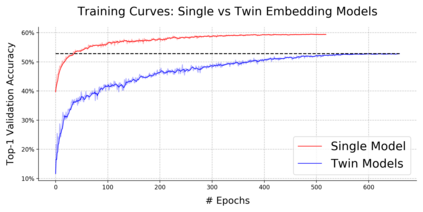
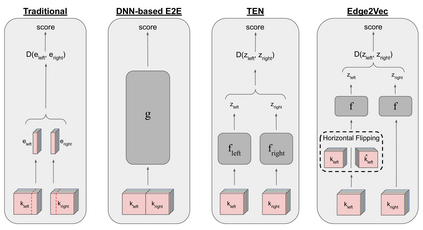
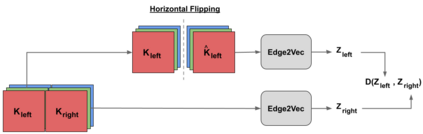
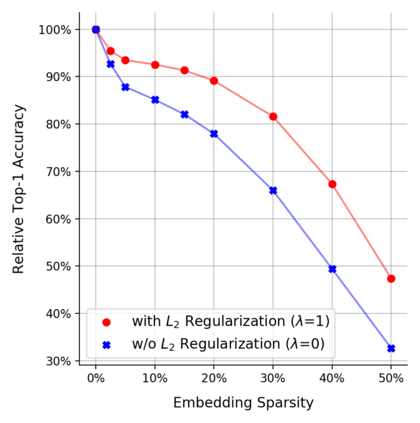
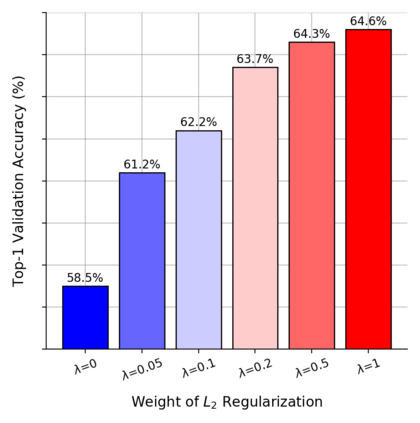
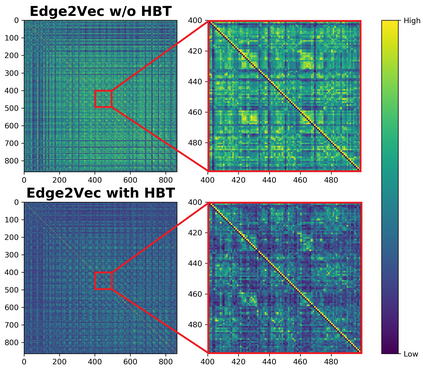
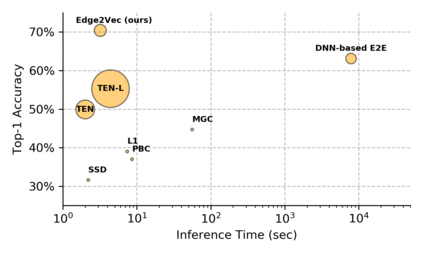
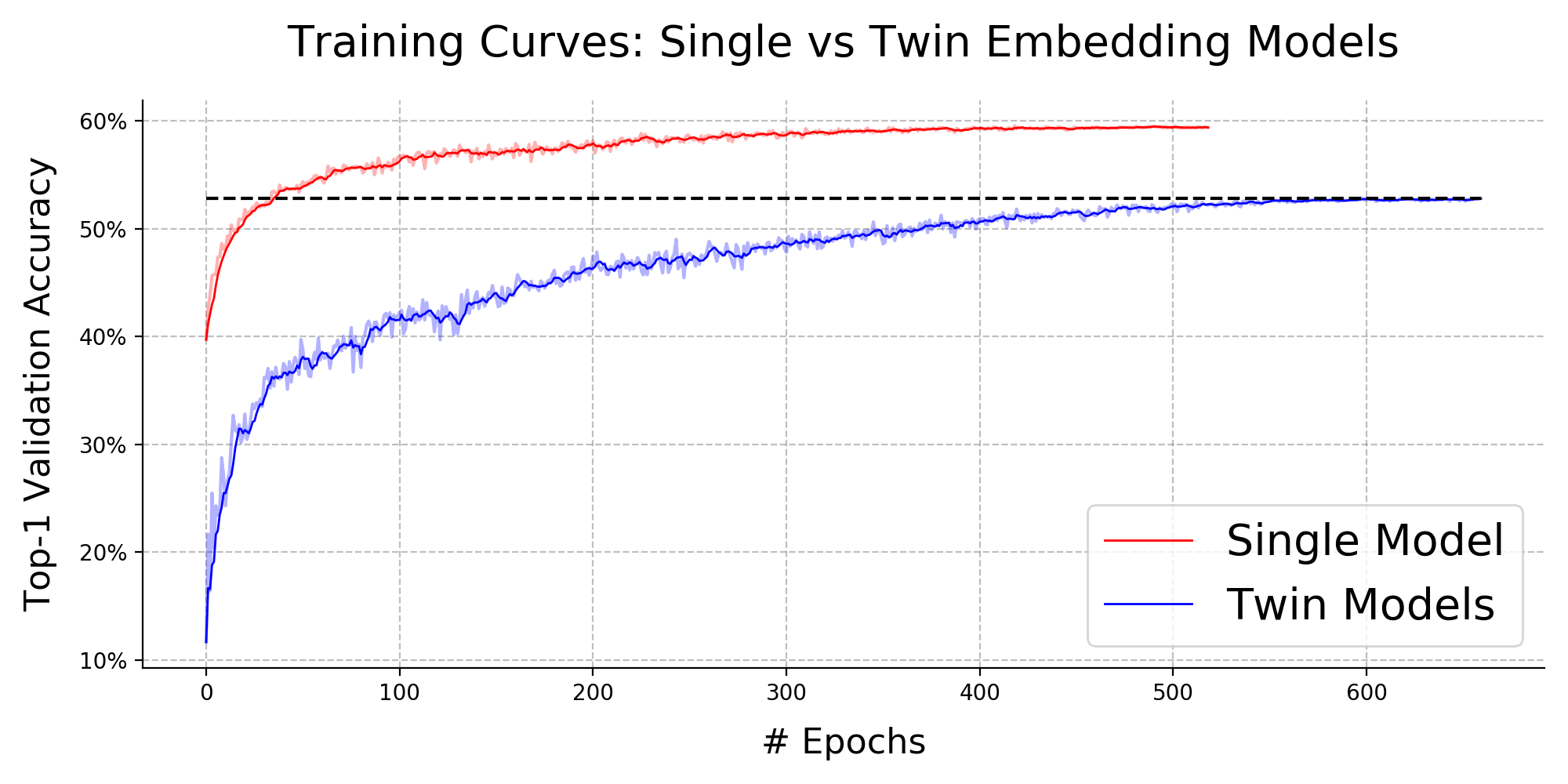
Pairwise compatibility measure (CM) is a key component in solving the jigsaw puzzle problem (JPP) and many of its recently proposed variants. With the rapid rise of deep neural networks (DNNs), a trade-off between performance (i.e., accuracy) and computational efficiency has become a very significant issue. Whereas an end-to-end DNN-based CM model exhibits high performance, it becomes virtually infeasible on very large puzzles, due to its highly intensive computation. On the other hand, exploiting the concept of embeddings to alleviate significantly the computational efficiency, has resulted in degraded performance, according to recent studies. This paper derives an advanced CM model (based on modified embeddings and a new loss function, called hard batch triplet loss) for closing the above gap between speed and accuracy; namely a CM model that achieves SOTA results in terms of performance and efficiency combined. We evaluated our newly derived CM on three commonly used datasets, and obtained a reconstruction improvement of 5.8% and 19.5% for so-called Type-1 and Type-2 problem variants, respectively, compared to best known results due to previous CMs.
翻译:以端到端 DNN CM 模型显示,该模型的性能很高,但在非常大的拼图上却几乎行不通,因为它的计算非常密集。另一方面,利用嵌入概念大大降低计算效率,根据最近的研究,导致性能下降,根据最近的研究,该论文产生了一种先进的CM模型(以经修改的嵌入和新的损失函数为基础,称为硬批次三重损失),用于缩小速度和准确性之间的上述差距;即实现SOTA结果的CM模型,其性能和效率加在一起。我们用三种常用数据集对新获得的CM进行了评估,并分别对所谓的型号-1和型号2问题变量进行了5.8%和19.5%的重建改进,与以前已知最佳的CMM结果相比。