Safety-Critical Modular Deep Reinforcement Learning with Temporal Logic through Gaussian Processes and Control Barrier Functions

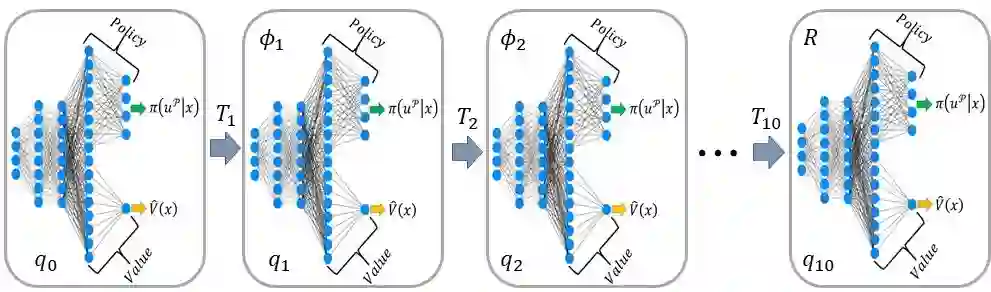
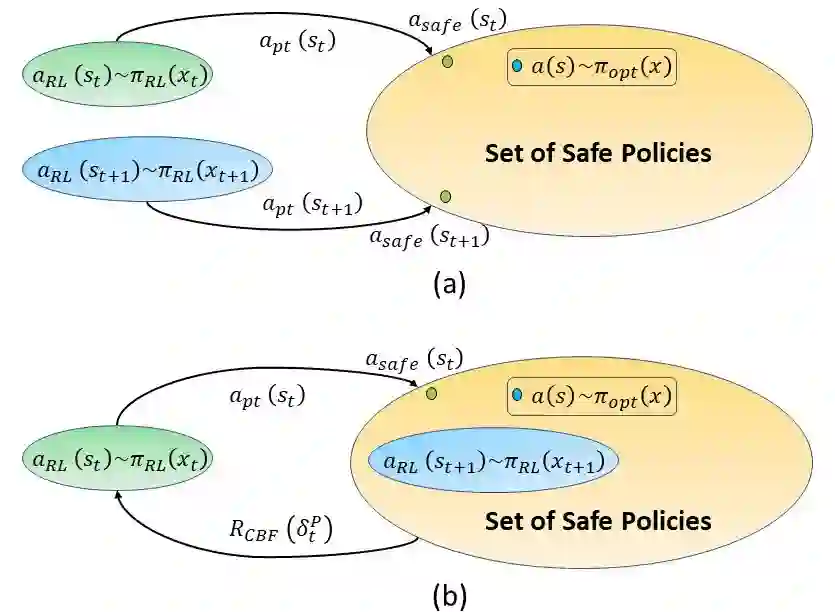
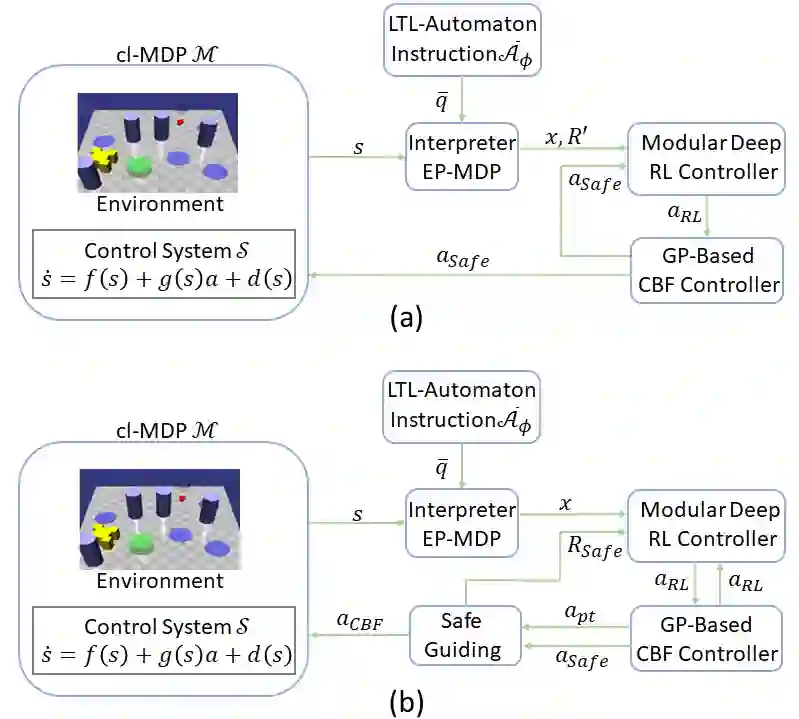
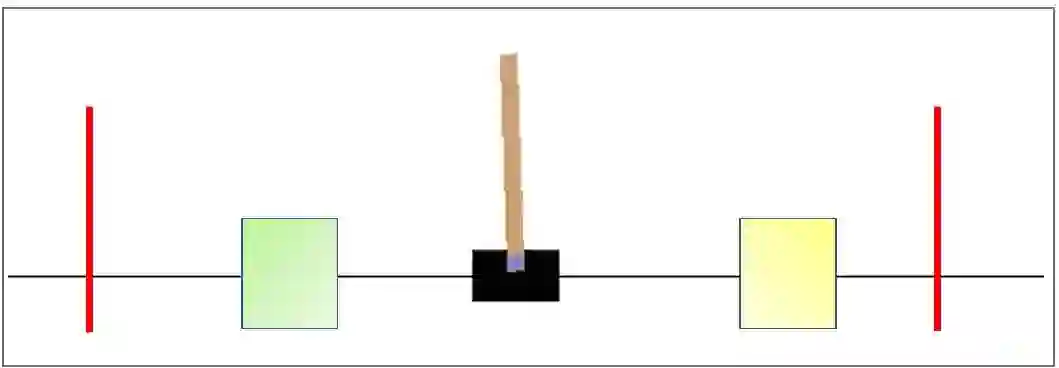
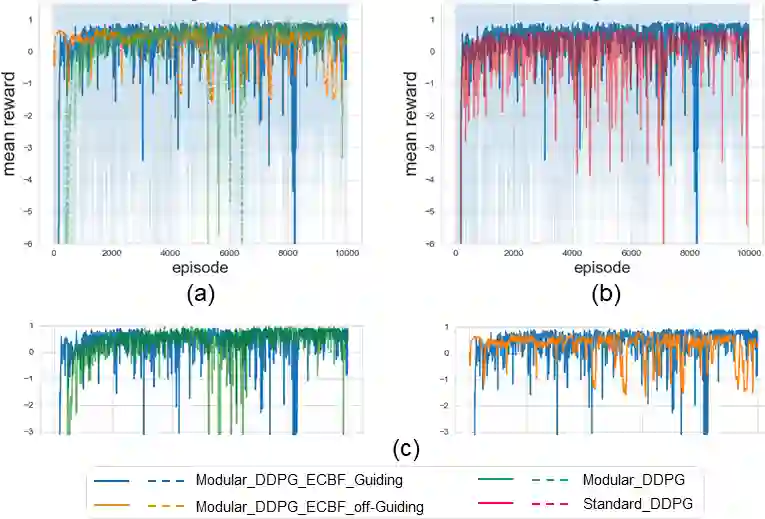
Reinforcement learning (RL) is a promising approach and has limited success towards real-world applications, because ensuring safe exploration or facilitating adequate exploitation is a challenge for controlling robotic systems with unknown models and measurement uncertainties. Such a learning problem becomes even more intractable for complex tasks over continuous space (state-space and action-space). In this paper, we propose a learning-based control framework consisting of several aspects: (1) linear temporal logic (LTL) is leveraged to facilitate complex tasks over an infinite horizons which can be translated to a novel automaton structure; (2) we propose an innovative reward scheme for RL-agent with the formal guarantee such that global optimal policies maximize the probability of satisfying the LTL specifications; (3) based on a reward shaping technique, we develop a modular policy-gradient architecture utilizing the benefits of automaton structures to decompose overall tasks and facilitate the performance of learned controllers; (4) by incorporating Gaussian Processes (GPs) to estimate the uncertain dynamic systems, we synthesize a model-based safeguard using Exponential Control Barrier Functions (ECBFs) to address problems with high-order relative degrees. In addition, we utilize the properties of LTL automatons and ECBFs to construct a guiding process to further improve the efficiency of exploration. Finally, we demonstrate the effectiveness of the framework via several robotic environments. And we show such an ECBF-based modular deep RL algorithm achieves near-perfect success rates and guard safety with a high probability confidence during training.