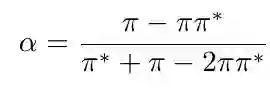Positive-Unlabeled Classification under Class Prior Shift and Asymmetric Error

A bottleneck of binary classification from positive and unlabeled data (PU classification) is the requirement that given unlabeled patterns are drawn from the same distribution as the test distribution. However, such a requirement is often not fulfilled in practice. In this paper, we generalize PU classification to the class prior shift scenario, where the class prior of given unlabeled patterns is different from that of test unlabeled patterns. Based on the analysis of the Bayes optimal classifier, we show that given a test class prior, PU classification under class prior shift is equivalent to PU classification with asymmetric error, where the false positive penalty and the false negative penalty are different. Then, we propose two frameworks to handle these problems, namely, a risk minimization framework and density ratio estimation framework. Finally, we demonstrate the effectiveness of the proposed frameworks and compare both frameworks through experiments using benchmark datasets.