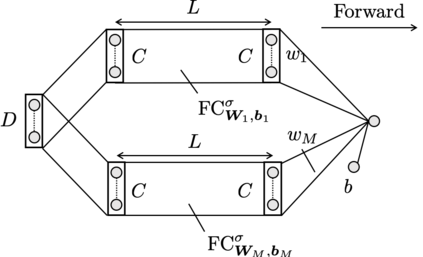
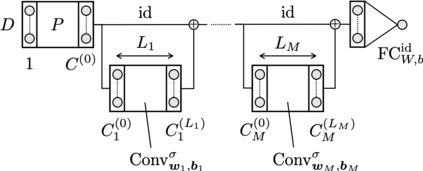
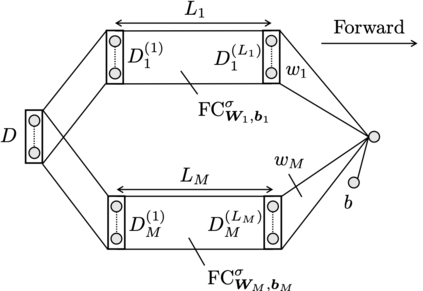
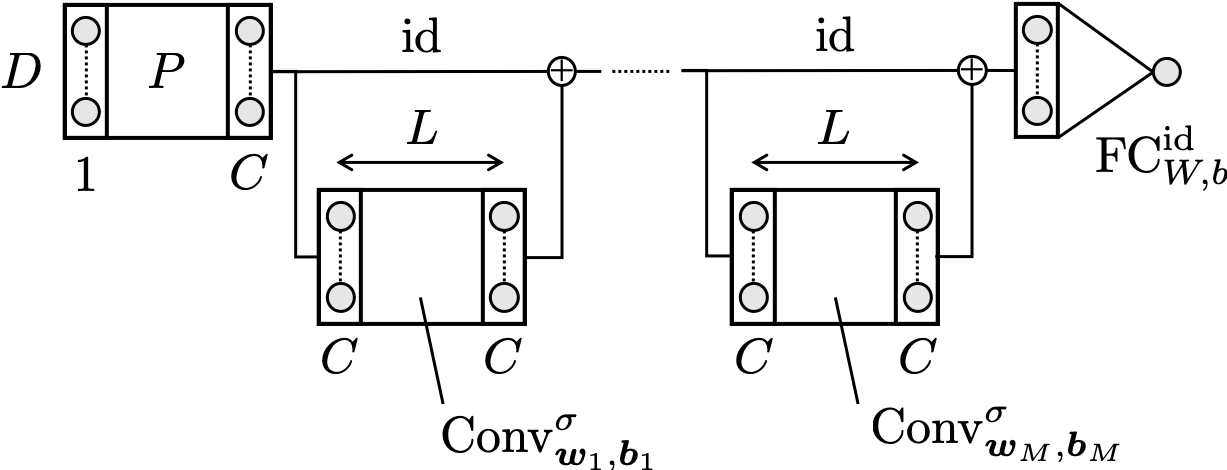
Convolutional neural networks (CNNs) have been shown to achieve optimal approximation and estimation error rates (in minimax sense) in several function classes. However, previous analyzed optimal CNNs are unrealistically wide and difficult to obtain via optimization due to sparse constraints in important function classes, including the H\"older class. We show a ResNet-type CNN can attain the minimax optimal error rates in these classes in more plausible situations -- it can be dense, and its width, channel size, and filter size are constant with respect to sample size. The key idea is that we can replicate the learning ability of Fully-connected neural networks (FNNs) by tailored CNNs, as long as the FNNs have \textit{block-sparse} structures. Our theory is general in a sense that we can automatically translate any approximation rate achieved by block-sparse FNNs into that by CNNs. As an application, we derive approximation and estimation error rates of the aformentioned type of CNNs for the Barron and H\"older classes with the same strategy.
翻译:在几个功能类中,显示进化神经网络(CNN)可以达到最佳近似率和估计误差率(迷你式),然而,由于包括H\'older类在内的重要功能类中的限制稀少,先前分析过的最佳有线电视新闻网(CNN)不切实际,很难通过优化获得。我们展示了ResNet型有线电视新闻网能够在更合理的情况下达到这些类中的微小最大最佳误差率 -- -- 它可能密度大,其宽度、频道大小和过滤器大小与样本大小不相上下。关键的想法是,只要有专门设计的有线电视新闻网(FNNN),只要FNNs有\text{block-spassy}结构,我们就可以复制全连通的神经网络(FNNNW)的学习能力。我们的理论很笼统,我们可以自动将区块型FNNNS达到的任何近似率转化为CNNN。作为一个应用,我们用同样的策略来得出上述类型的CNNNNN的近似误率和估计误率。