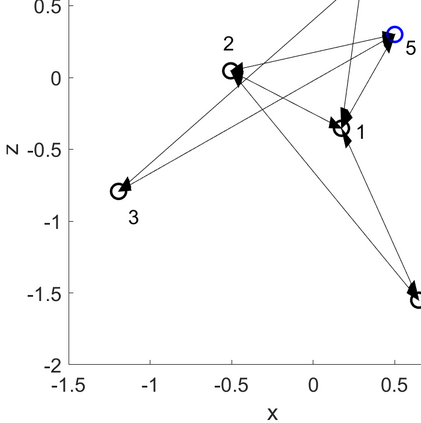
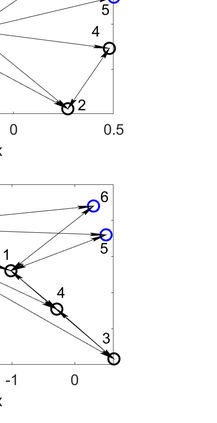
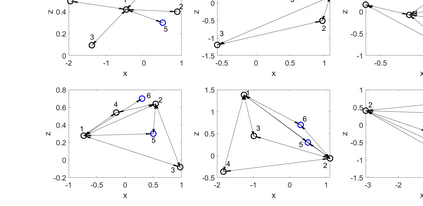
One of the well-known challenges in optimal experimental design is how to efficiently estimate the nested integrations of the expected information gain. The Gaussian approximation and associated importance sampling have been shown to be effective at reducing the numerical costs. However, they may fail due to the non-negligible biases and the numerical instabilities. A new approach is developed to compute the expected information gain, when the posterior distribution is multimodal - a situation previously ignored by the methods aiming at accelerating the nested numerical integrations. Specifically, the posterior distribution is approximated using a mixture distribution constructed by multiple runs of global search for the modes and weighted local Laplace approximations. Under any given probability of capturing all the modes, we provide an estimation of the number of runs of searches, which is dimension independent. It is shown that the novel global-local multimodal approach can be significantly more accurate and more efficient than the other existing approaches, especially when the number of modes is large. The methods can be applied to the designs of experiments with both calibrated and uncalibrated observation noises.
翻译:最佳实验设计中众所周知的挑战之一是如何有效估计预期信息收益的嵌套整合情况。Gausian近似值和相关重要性抽样已证明在降低数字成本方面是有效的。然而,由于不可忽略的偏差和数字不稳定性,这些抽样可能无法奏效。开发了一种新的方法来计算预期信息收益,当事后分配是多式的时,即事后分配是多式的——以前被旨在加速嵌套数字整合的方法所忽视的一种情况。具体地说,后方分配是使用多种全球搜索方式和加权本地拉普尔近似值所构建的混合物分布的近似值。在捕捉所有模式的任何特定可能性下,我们提供了搜索运行次数的估计,这是独立的层面。这表明新的全球-地方多式联运方法比其他现有方法更加准确和高效,特别是当模式数量巨大时。这种方法可以适用于以校准和未校准的观测噪音进行实验的设计。