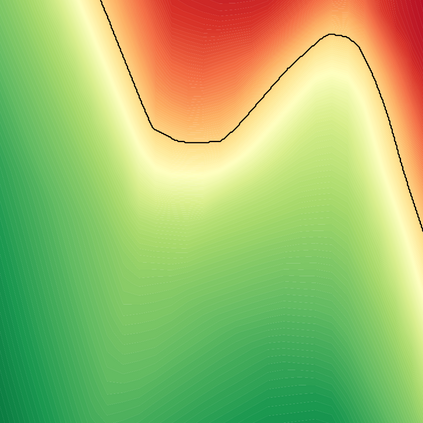
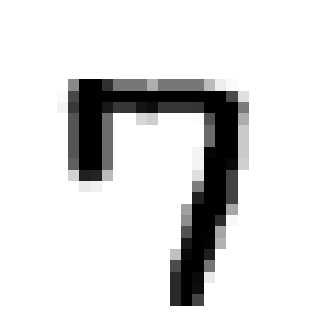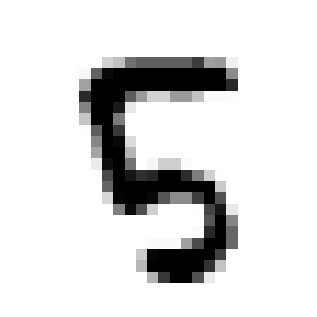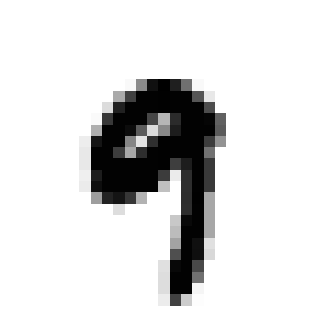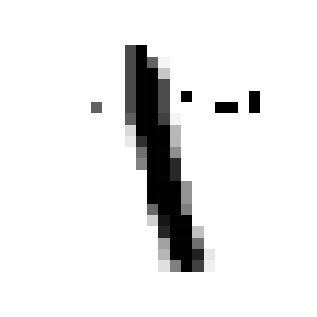Evaluating adversarial robustness amounts to finding the minimum perturbation needed to have an input sample misclassified. The inherent complexity of the underlying optimization requires current gradient-based attacks to be carefully tuned, initialized, and possibly executed for many computationally-demanding iterations, even if specialized to a given perturbation model. In this work, we overcome these limitations by proposing a fast minimum-norm (FMN) attack that works with different $\ell_p$-norm perturbation models ($p=0, 1, 2, \infty$), is robust to hyperparameter choices, does not require adversarial starting points, and converges within few lightweight steps. It works by iteratively finding the sample misclassified with maximum confidence within an $\ell_p$-norm constraint of size $\epsilon$, while adapting $\epsilon$ to minimize the distance of the current sample to the decision boundary. Extensive experiments show that FMN significantly outperforms existing attacks in terms of convergence speed and computation time, while reporting comparable or even smaller perturbation sizes.
翻译:在这项工作中,我们克服了这些限制,提出了快速最低调(FMN)攻击,该攻击以不同的美元=0, 1, 2, ninfty美元操作,对超参数选择十分可靠,不需要对抗性起点,也不需要少数轻量级步骤,而是需要仔细调整、初始化当前基于梯度的攻击,并可能对许多计算性需要的迭代执行,即使专门针对特定扰动模式。在这项工作中,我们提出了快速最小调控(FMN)攻击,用不同的美元=_p$-norm perturbation 模型操作($=0, 1, 2,\infty$),从而克服了这些限制。广泛的实验表明,FMN在趋同速度和计算时间方面大大超过现有的攻击,同时报告可比较或更小的半调幅大小。