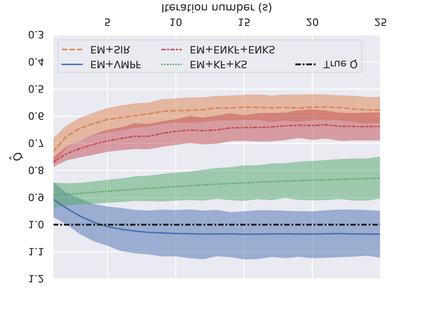
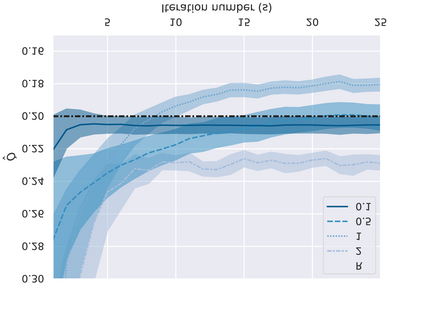
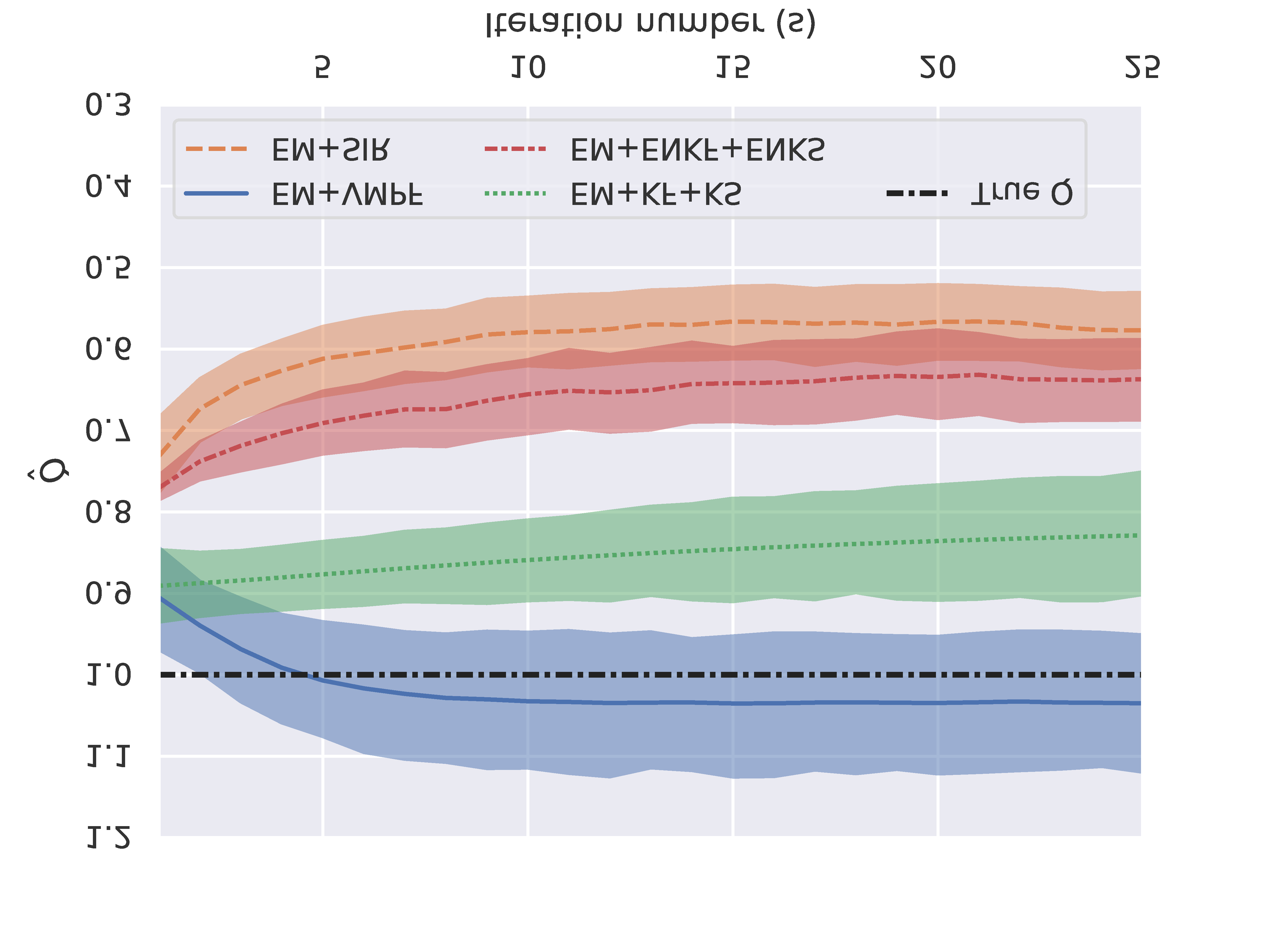
Model error covariances play a central role in the performance of data assimilation methods applied to nonlinear state-space models. However, these covariances are largely unknown in most of the applications. A misspecification of the model error covariance has a strong impact on the computation of the posterior probability density function, leading to unreliable estimations and even to a total failure of the assimilation procedure. In this work, we propose the combination of the Expectation-Maximization algorithm (EM) with an efficient particle filter to estimate the model error covariance, using a batch of observations. Based on the EM algorithm principles, the proposed method encompasses two stages: the expectation stage, in which a particle filter is used with the present estimate of the model error covariance as given to find the probability density function that maximizes the likelihood, followed by a maximization stage in which the expectation under the probability density function found in the expectation step is maximized as a function of the elements of the model error covariance. This novel algorithm here presented combines the EM with a fixed point algorithm and does not require a particle smoother to approximate the posterior densities. We demonstrate that the new method accurately and efficiently solves the linear model problem. Furthermore, for the chaotic nonlinear Lorenz-96 model the method is stable even for observation error covariance 10 times larger than the estimated model error covariance matrix, and also that it is successful in high-dimensional situations where the dimension of the estimated matrix is 1600.
翻译:模型误差常量在用于非线性状态空间模型的数据同化方法的性能中起着中心作用。 但是, 这些共差在大多数应用中基本上并不为人所知。 模型误差常量的偏差对计算后数概率密度函数产生强烈的影响, 导致估算不可靠, 甚至同化程序完全失败。 在这项工作中, 我们提议将期望- 最大化算法与高效粒子过滤器相结合, 以利用一组观察来估计模型误差异差值。 根据EM 算法原则, 提议的方法包括两个阶段: 期望阶段, 使用粒子过滤器与目前对模型误差共变值的估算相匹配, 以找到最大可能性的概率密度函数, 之后的最小化阶段, 在预期步骤中发现的概率密度函数中, 最大值是模型误差度大小的函数。 此处展示的新的EM 与固定点运算法, 不需要粒子平滑度的状态, 并且不需要在新的解度模型中测算法中, 也显示新的解度误差值。