Closed-form portfolio optimization under GARCH models

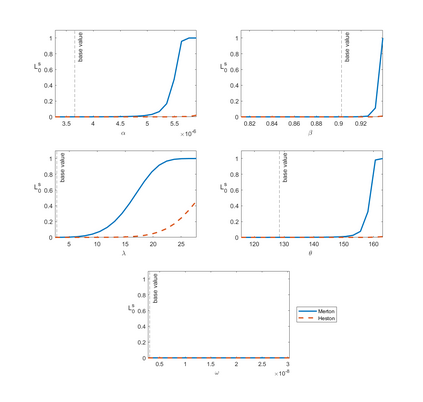
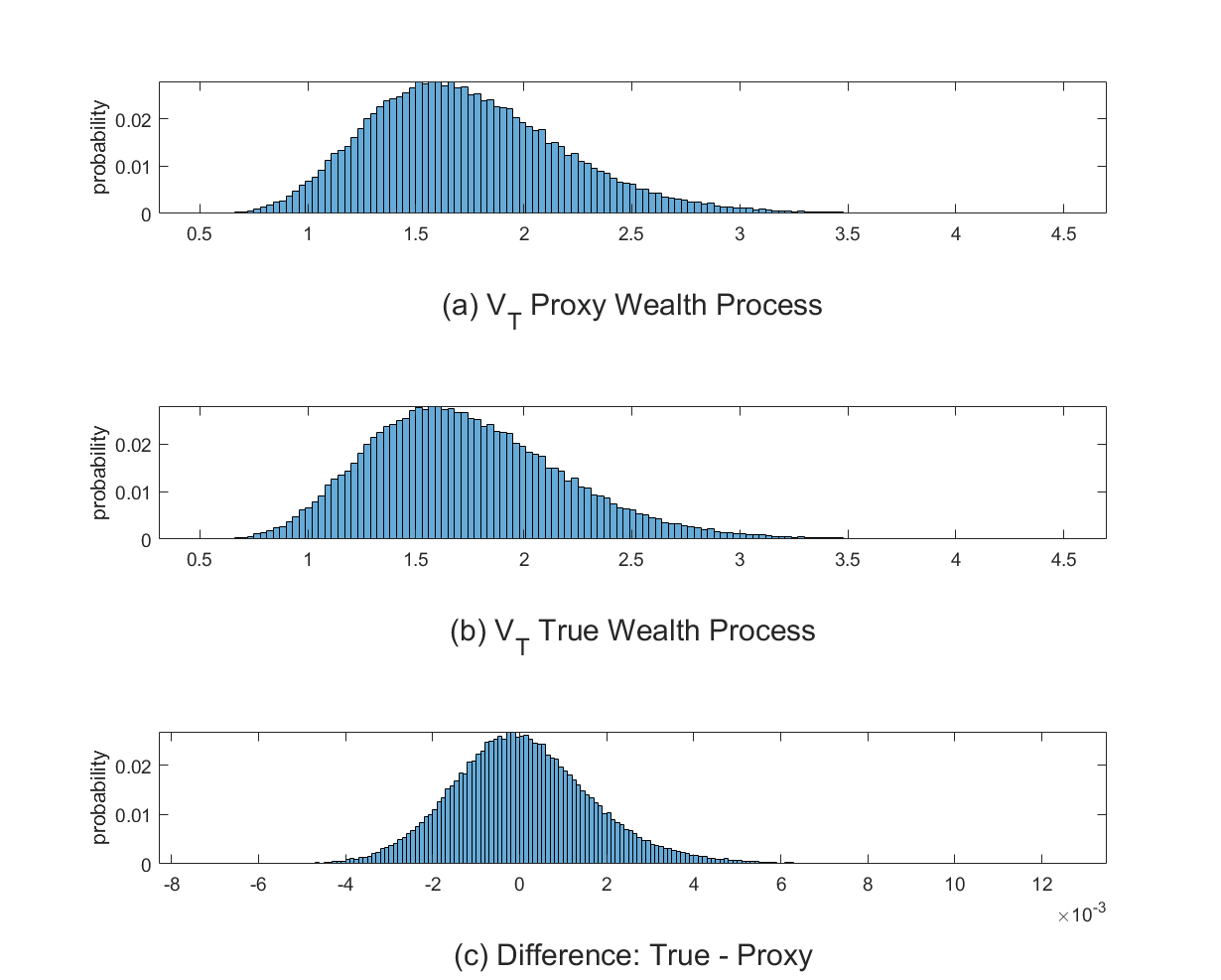
This paper develops the first closed-form optimal portfolio allocation formula for a spot asset whose variance follows a GARCH(1,1) process. We consider an investor with constant relative risk aversion (CRRA) utility who wants to maximize the expected utility from terminal wealth under a Heston and Nandi (2000) GARCH (HN-GARCH) model. We obtain closed formulas for the optimal investment strategy, the value function and the optimal terminal wealth. We find the optimal strategy is independent of the development of the risky asset, and the solution converges to that of a continuous-time Heston stochastic volatility model, albeit under additional conditions. For a daily trading scenario, the optimal solutions are quite robust to variations in the parameters, while the numerical wealth equivalent loss (WEL) analysis shows good performance of the Heston solution, with a quite inferior performance of the Merton solution.