Hierarchical Control for Cooperative Teams in Competitive Autonomous Racing

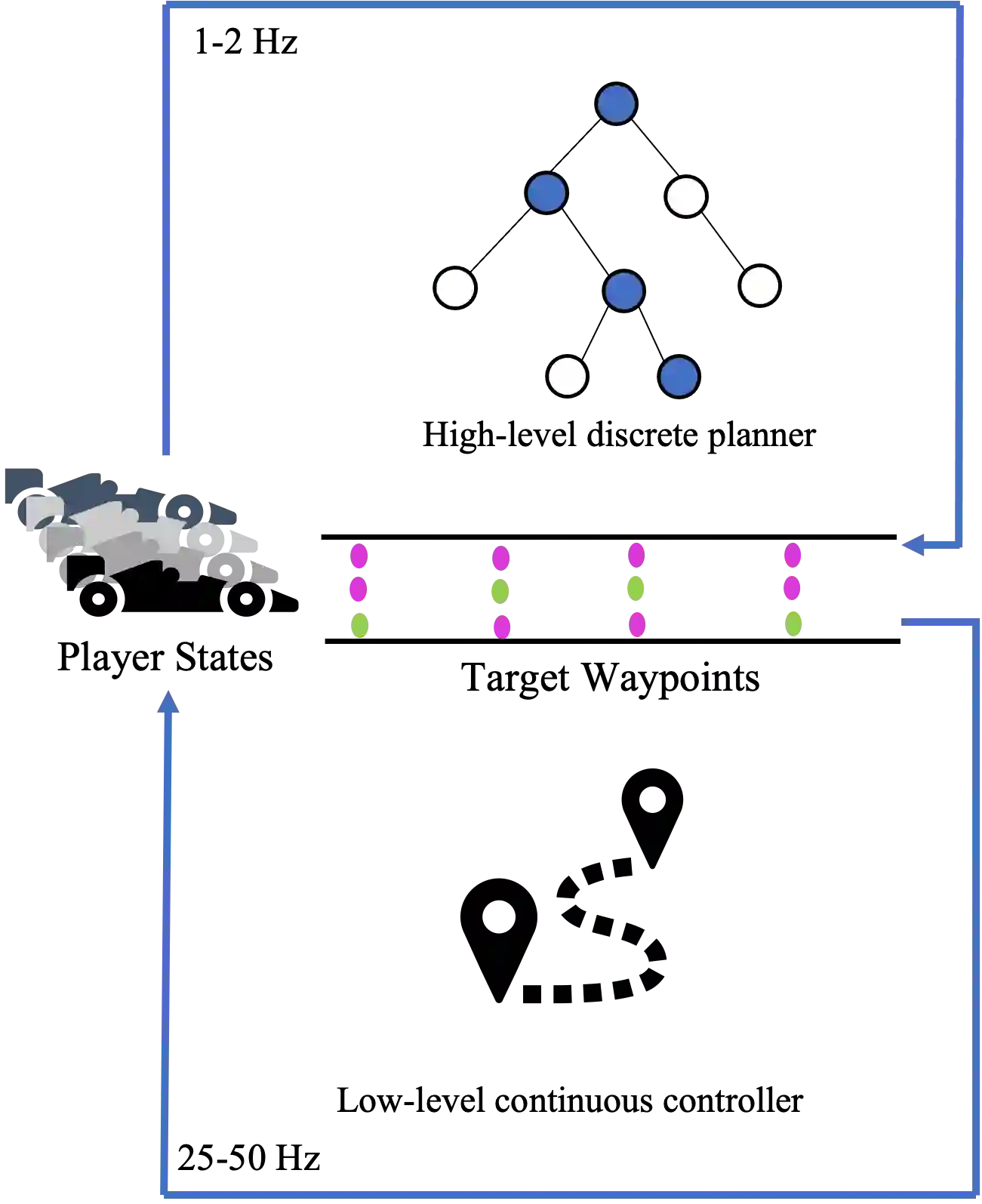
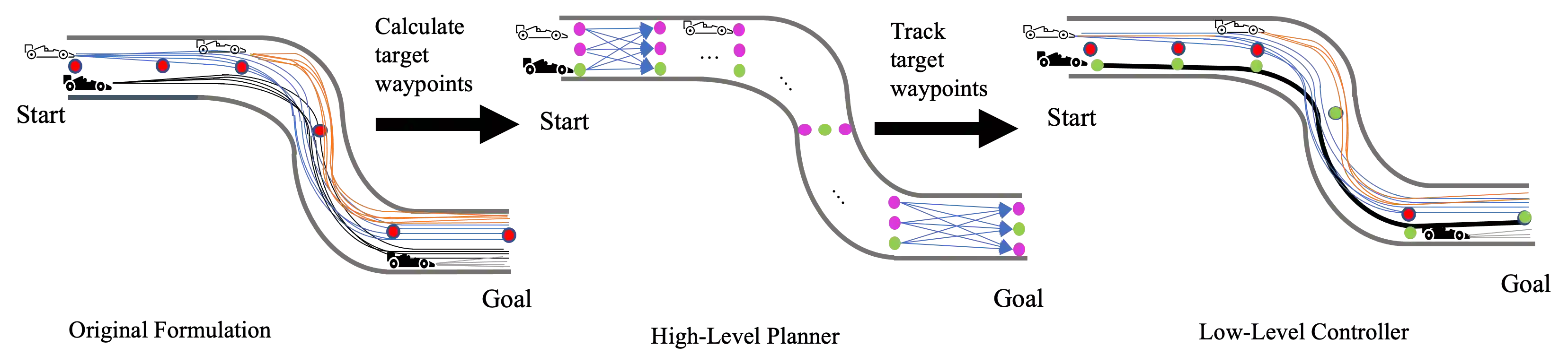
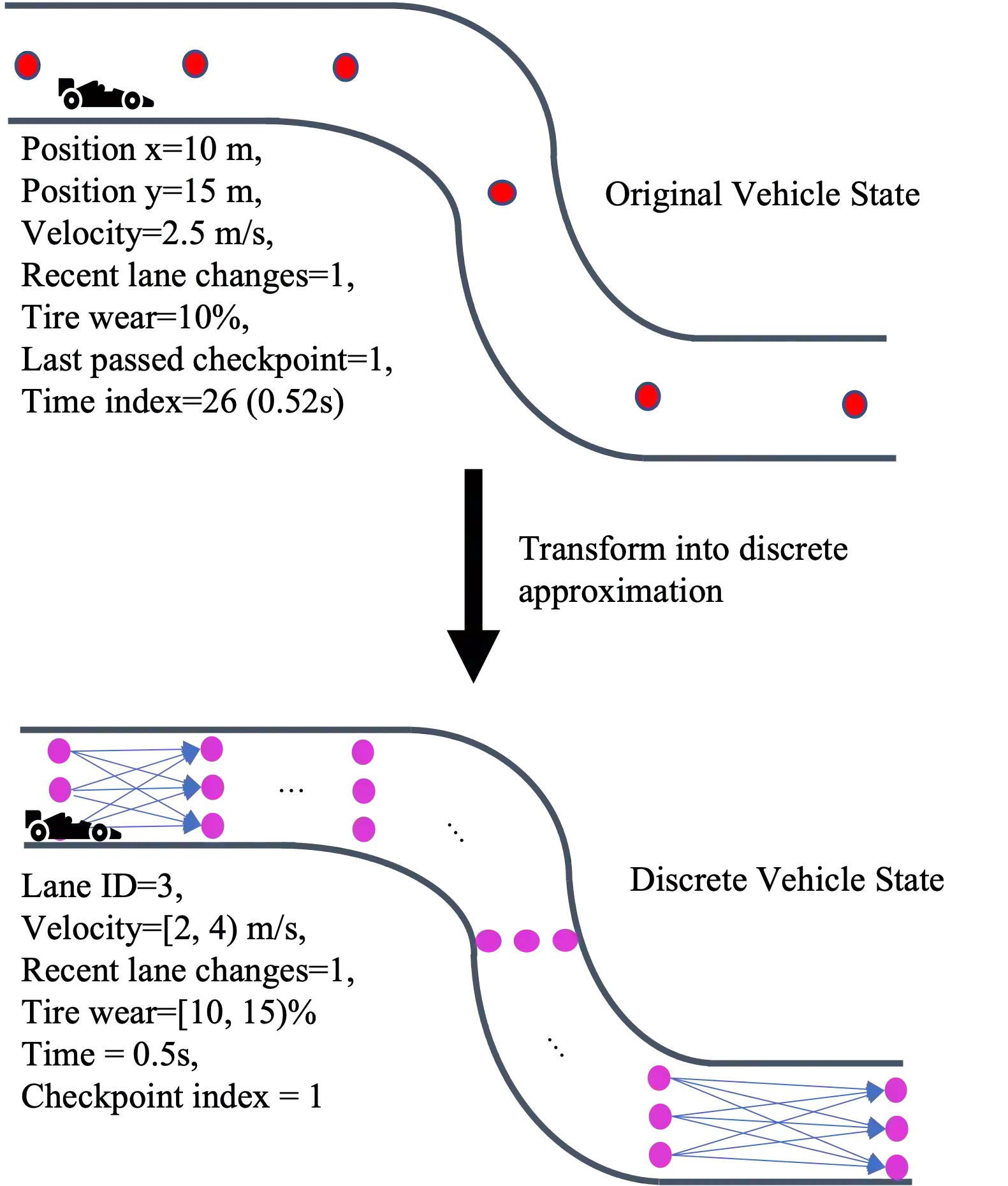
We study the problem of autonomous racing amongst teams composed of cooperative agents subject to realistic safety and fairness rules. We develop a hierarchical controller to solve this problem consisting of two levels, extending prior work where bi-level hierarchical control is applied to head-to-head autonomous racing. A high-level planner constructs a discrete game that encodes the complex rules with simplified dynamics to produce a sequence of target waypoints. The low-level controller uses the resulting waypoints as a reference trajectory and computes high-resolution control inputs by solving a simplified racing game with a reduced set of rules. We consider two approaches for the low-level planner: training a multi-agent reinforcement learning (MARL) policy and solving a linear-quadratic Nash game (LQNG) approximation. We test our controllers against three baselines on a simple oval track and a complex track: an end-to-end MARL controller, a MARL controller tracking a fixed racing line, and an LQNG controller tracking a fixed racing line. Quantitative results show that our hierarchical methods outperform their respective baseline methods in terms of race wins, overall team performance, and abiding by the rules. Qualitatively, we observe the hierarchical controllers mimicking actions performed by expert human drivers such as coordinated overtaking moves, defending against multiple opponents, and long-term planning for delayed advantages. We show that hierarchical planning for game-theoretic reasoning produces both cooperative and competitive behavior even when challenged with complex rules and constraints.