Geometry-informed irreversible perturbations for accelerated convergence of Langevin dynamics

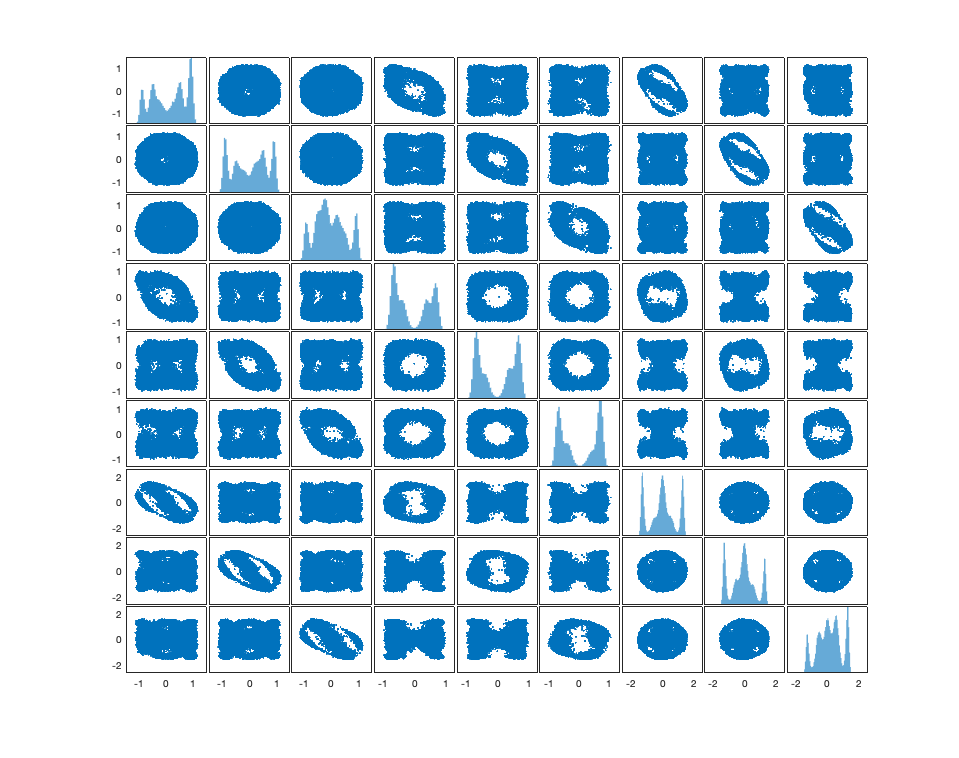
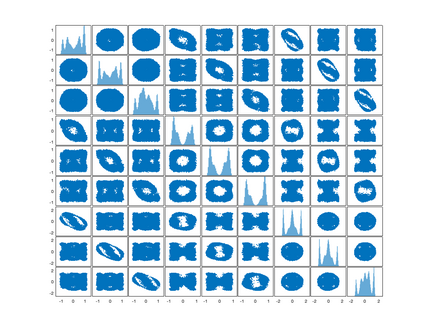
We introduce a novel geometry-informed irreversible perturbation that accelerates convergence of the Langevin algorithm for Bayesian computation. It is well documented that there exist perturbations to the Langevin dynamics that preserve its invariant measure while accelerating its convergence. Irreversible perturbations and reversible perturbations (such as Riemannian manifold Langevin dynamics (RMLD)) have separately been shown to improve the performance of Langevin samplers. We consider these two perturbations simultaneously by presenting a novel form of irreversible perturbation for RMLD that is informed by the underlying geometry. Through numerical examples, we show that this new irreversible perturbation can improve performance of the estimator over reversible perturbations that do not take the geometry into account. Moreover we demonstrate that irreversible perturbations generally can be implemented in conjunction with the stochastic gradient version of the Langevin algorithm. Lastly, while continuous-time irreversible perturbations cannot impair the performance of a Langevin estimator, the situation can sometimes be more complicated when discretization is considered. To this end, we describe a discrete-time example in which irreversibility increases both the bias and variance of the resulting estimator.