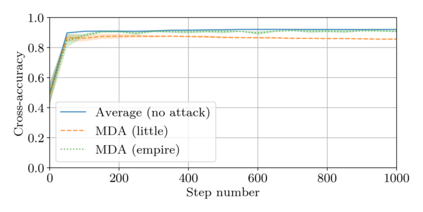
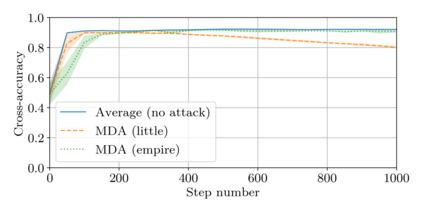
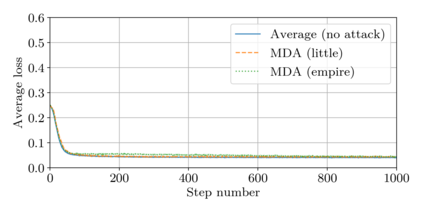
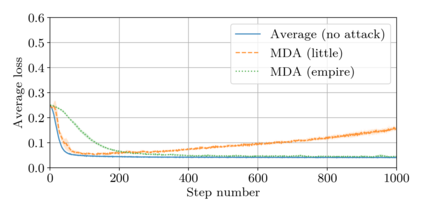
This paper addresses the problem of combining Byzantine resilience with privacy in machine learning (ML). Specifically, we study if a distributed implementation of the renowned Stochastic Gradient Descent (SGD) learning algorithm is feasible with both differential privacy (DP) and $(\alpha,f)$-Byzantine resilience. To the best of our knowledge, this is the first work to tackle this problem from a theoretical point of view. A key finding of our analyses is that the classical approaches to these two (seemingly) orthogonal issues are incompatible. More precisely, we show that a direct composition of these techniques makes the guarantees of the resulting SGD algorithm depend unfavourably upon the number of parameters of the ML model, making the training of large models practically infeasible. We validate our theoretical results through numerical experiments on publicly-available datasets; showing that it is impractical to ensure DP and Byzantine resilience simultaneously.
翻译:本文探讨了Byzantine应变能力与机器学习隐私相结合的问题。 具体地说,我们研究的是,如果分散实施著名的Stochatic Gradientle Grounds(SGD)学习算法,在有区别的隐私(DP)和$(alpha,f)美元-Byzantine两种情况下都是可行的。 据我们所知,这是从理论角度解决这一问题的第一个工作。我们分析的一个重要发现是,对这两个(似乎)正统问题的典型方法不相容。更确切地说,我们表明,这些技术的直接构成使得由此产生的SGD算法的保障不取决于ML模型的参数数量,使得大型模型的培训实际上不可行。我们通过在公开的数据集上进行数字实验来验证我们的理论结果;表明,确保DP和Byzantine同时具有复原力是不切实际的。