A Newton's Iteration Converges Quadratically to Nonisolated Solutions Too

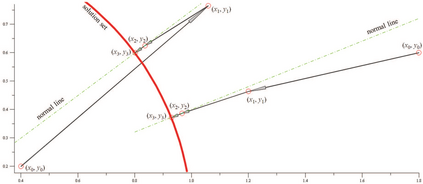
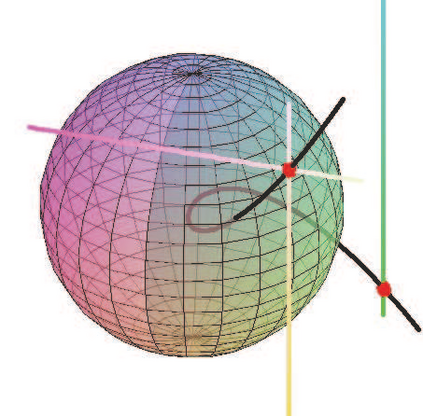
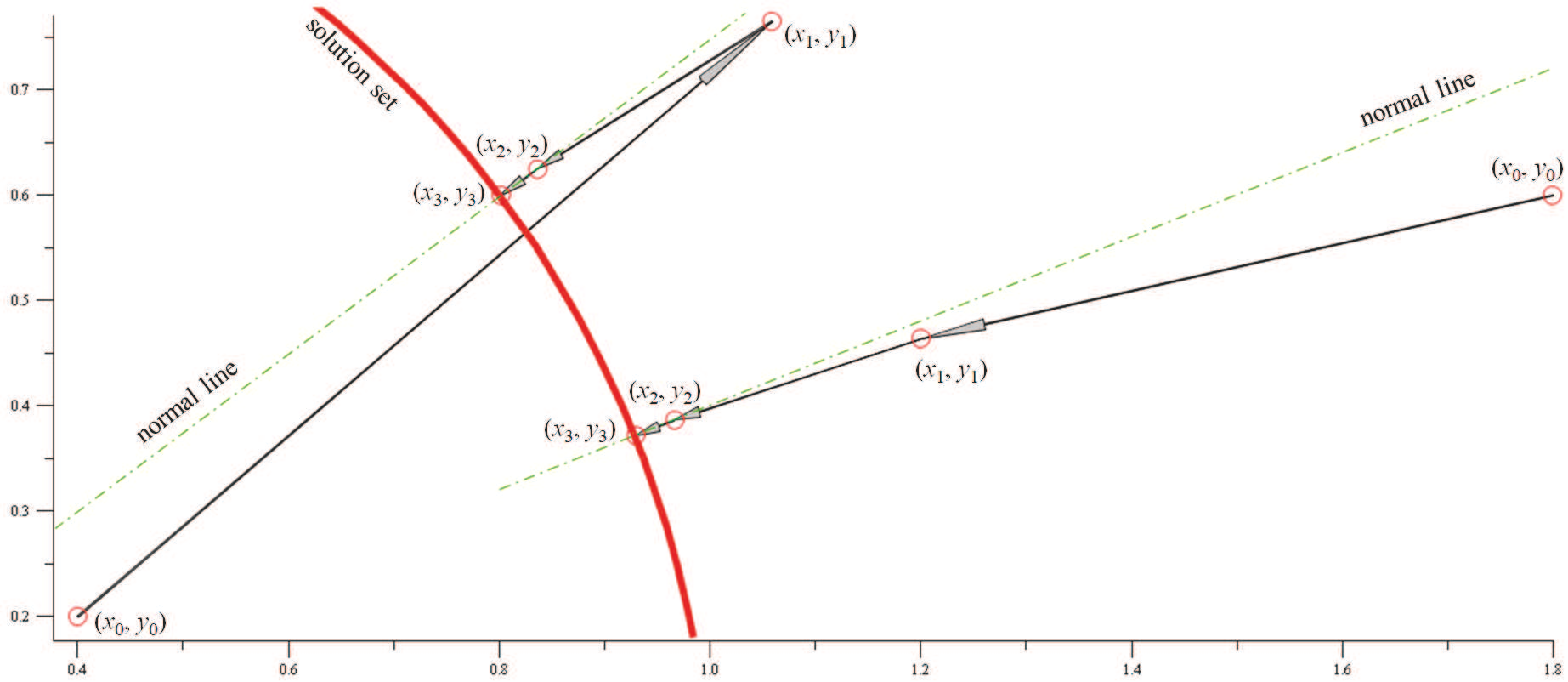
The textbook Newton's iteration is practically inapplicable on nonisolated solutions of unregularized nonlinear systems. With a simple modification, a version of Newton's iteration regains its local quadratic convergence to nonisolated zeros of smooth mappings assuming the solutions are semiregular as properly defined regardless of whether the system is square, underdetermined or overdetermined. Furthermore, the iteration serves as a de facto regularization mechanism for computing singular zeros from empirical data. Even if the given system is perturbed so that the nonisolated solution disappears, the iteration still locally converges to a stationary point that approximates a solution of the underlying system with an error bound in the same order of the data accuracy. Geometrically, the iteration approximately converges to the nearest point on the solution manifold. This extension simplifies nonlinear system modeling by eliminating the zero isolation process and enables a wide range of applications in algebraic computation.