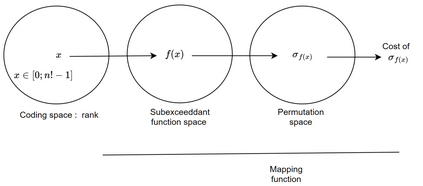
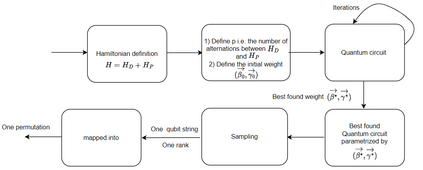
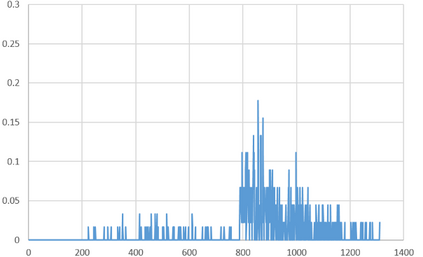
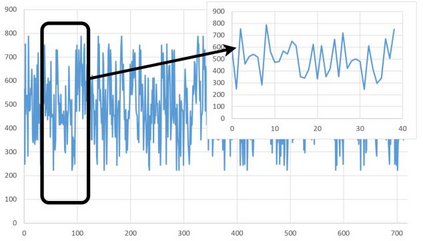
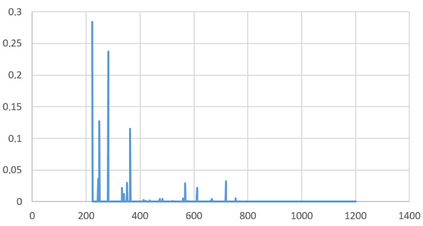
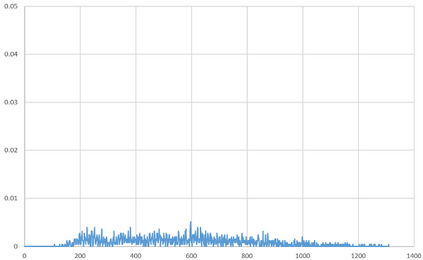
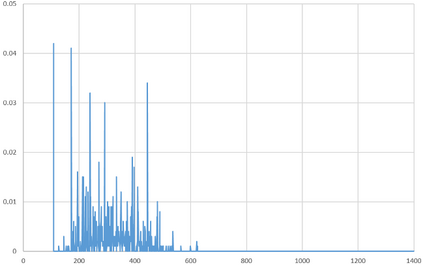
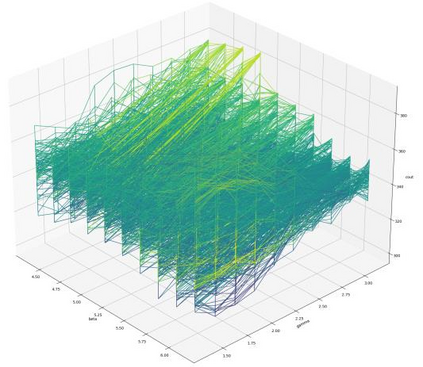
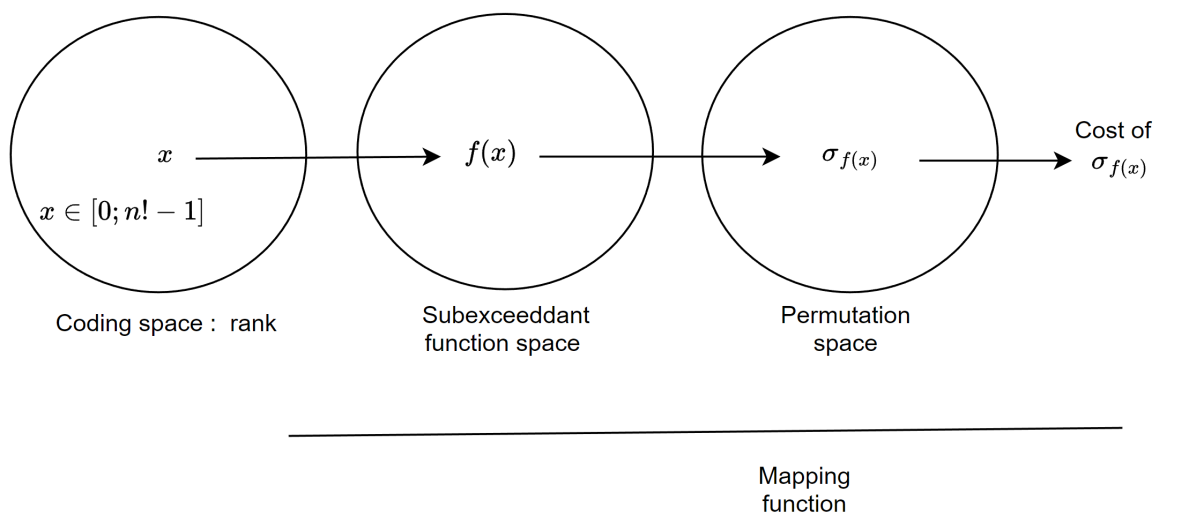
We propose an Indirect Quantum Approximate Optimization Algorithm (referred to as IQAOA) where the Quantum Alternating Operator Ansatz takes into consideration a general parameterized family of unitary operators to efficiently model the Hamiltonian describing the set of string vectors. This algorithm creates an efficient alternative to QAOA, where: 1) a Quantum parametrized circuit executed on a quantum machine models the set of string vectors; 2) a Classical meta-optimization loop executed on a classical machine; 3) an estimation of the average cost of each string vector computing, using a well know algorithm coming from the OR community that is problem dependent. The indirect encoding defined by dimensional string vector is mapped into a solution by an efficient coding/decoding mechanism. The main advantage is to obtain a quantum circuit with a strongly limited number of gates that could be executed on the noisy current quantum machines. The numerical experiments achieved with IQAOA permits to solve 8-customer instances TSP using the IBM simulator which are to the best of our knowledge the largest TSP ever solved using a QAOA based approach.
翻译:暂无翻译