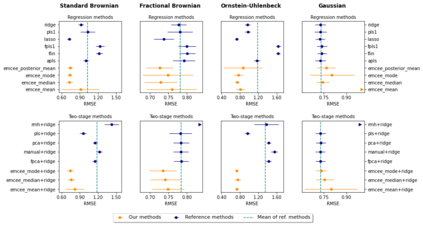
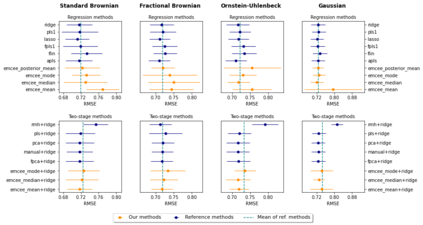
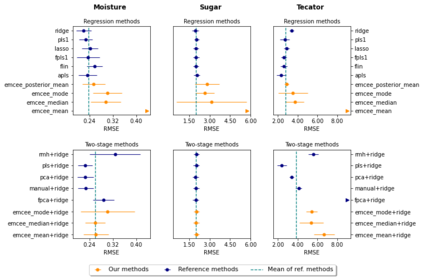
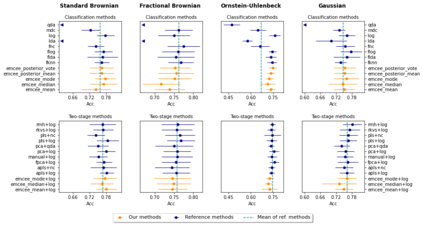
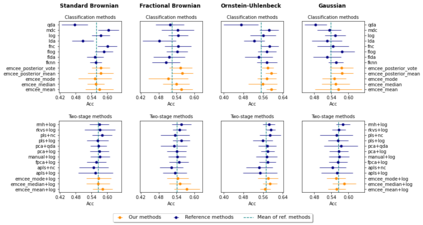
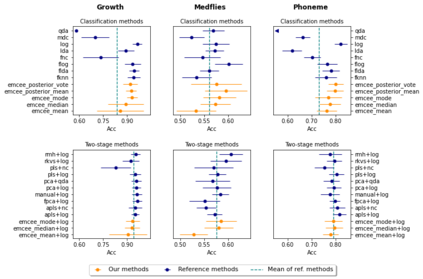
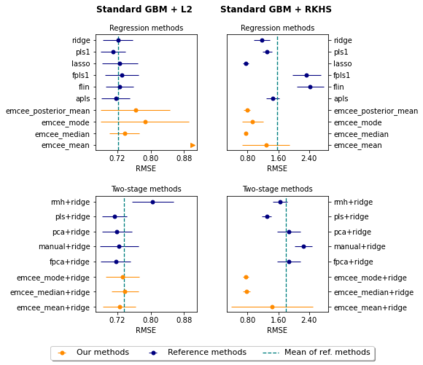
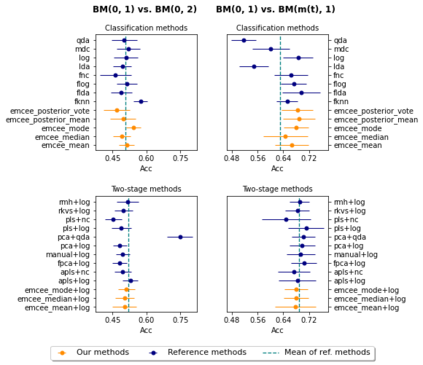
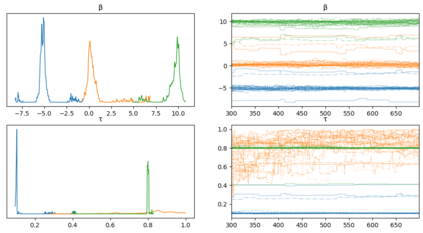
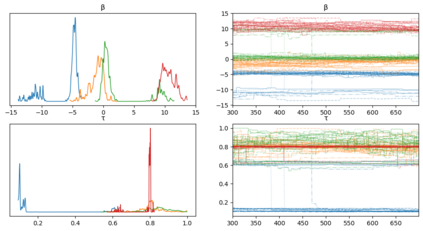
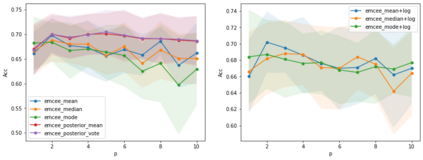
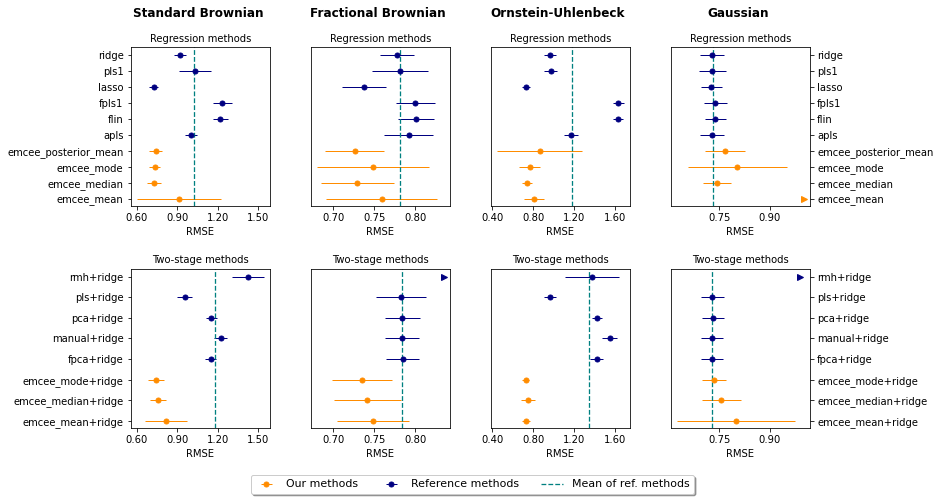
We propose a novel Bayesian methodology for inference in functional linear and logistic regression models based on the theory of reproducing kernel Hilbert spaces (RKHS's). These models build upon the RKHS associated with the covariance function of the underlying stochastic process, and can be viewed as a finite-dimensional approximation to the classical functional regression paradigm. The corresponding functional model is determined by a function living on a dense subspace of the RKHS of interest, which has a tractable parametric form based on linear combinations of the kernel. By imposing a suitable prior distribution on this functional space, we can naturally perform data-driven inference via standard Bayes methodology, estimating the posterior distribution through Markov chain Monte Carlo (MCMC) methods. In this context, our contribution is two-fold. First, we derive a theoretical result that guarantees posterior consistency in these models, based on an application of a classic theorem of Doob to our RKHS setting. Second, we show that several prediction strategies stemming from our Bayesian formulation are competitive against other usual alternatives in both simulations and real data sets, including a Bayesian-motivated variable selection procedure.
翻译:暂无翻译