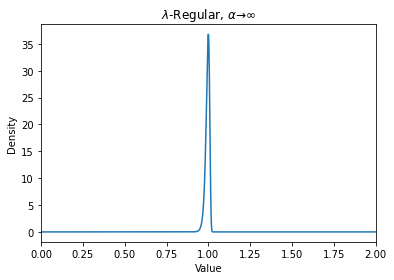
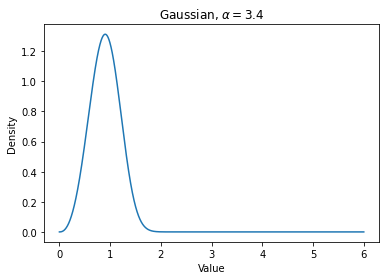
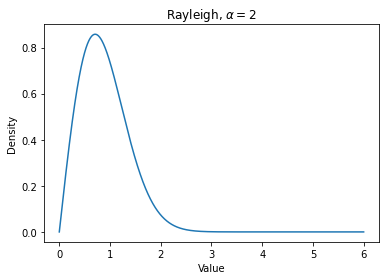
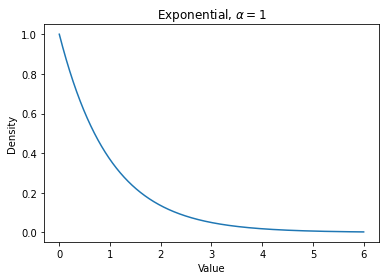
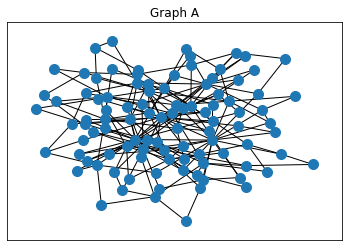
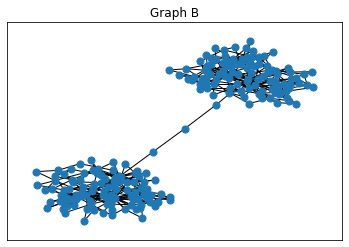
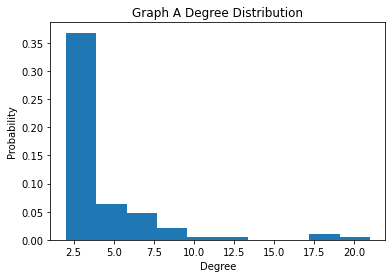
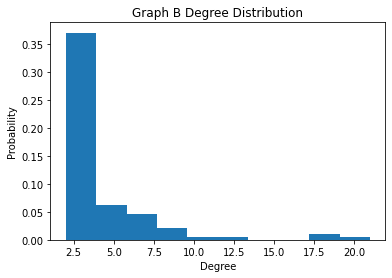
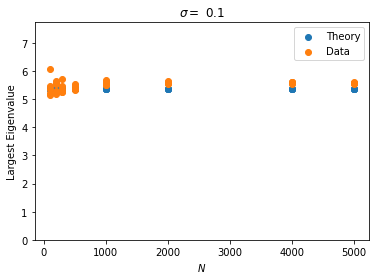
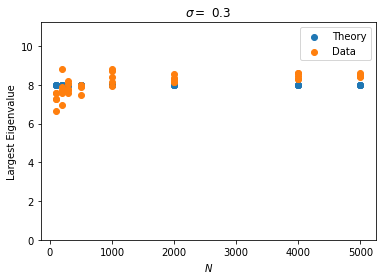
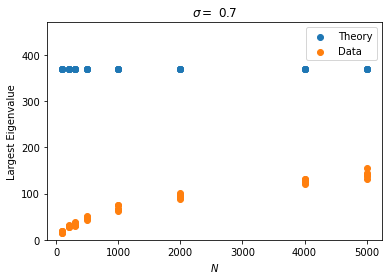
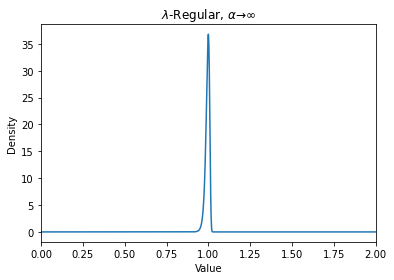
We present a simple method to quantitatively capture the heterogeneity in the degree distribution of a network graph using a single parameter $\sigma$. Using an exponential transformation of the shape parameter of the Weibull distribution, this control parameter allows the degree distribution to be easily interpolated between highly symmetric and highly heterogeneous distributions on the unit interval. This parameterization of heterogeneity also recovers several other canonical distributions as intermediate special cases, including the Gaussian, Rayleigh, and exponential distributions. We then outline a general graph generation algorithm to produce graphs with a desired amount of heterogeneity. The utility of this formulation of a heterogeneity parameter is demonstrated with examples relating to epidemiological modeling and spectral analysis.
翻译:我们提出了一个简单的方法,用单一参数 $\ sigma$ 来量化网络图分布度的异质性。使用Weibull分布的形状参数的指数转换,这个控制参数可以使该分布度在单位间隔高度对称和高度多样化分布之间容易地相互交错。这种异质性参数化还作为中间特殊案例,恢复了其他几种发光性分布,包括Gaussian、Rayleigh和指数分布。然后我们概述了一种一般的图形生成算法,以生成具有理想程度异质性的图表。这种配方的异质性参数的实用性在与流行病学建模和光谱分析有关的例子中得到了证明。