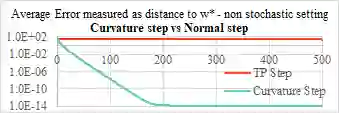
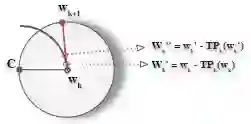
应用加强学习的超定线性系统规模变异解决方案 (Scale Invariant Solutions for Overdetermined Linear Systems with Applications to Reinforcement Learning)

Overdetermined linear systems are common in reinforcement learning, e.g., in Q and value function estimation with function approximation. The standard least-squares criterion, however, leads to a solution that is unduly influenced by rows with large norms. This is a serious issue, especially when the matrices in these systems are beyond user control. To address this, we propose a scale-invariant criterion that we then use to develop two novel algorithms for value function estimation: Normalized Monte Carlo and Normalized TD(0). Separately, we also introduce a novel adaptive stepsize that may be useful beyond this work as well. We use simulations and theoretical guarantees to demonstrate the efficacy of our ideas.

翻译：超定线性系统在强化学习中很常见,例如在Q和价值函数估算中,有功能近似值。标准最小平方标准导致一种不适当地受具有大规范的行影响的解决办法。这是一个严重的问题,特别是当这些系统中的矩阵超出用户控制范围时。为了解决这个问题,我们提出了一个规模变化性标准,然后我们用它来为价值函数估算制定两种新的算法:正常化的蒙特卡洛和正常化的TD(0),另外,我们还引入了一种新的适应步骤,这可能在这项工作之外有用。我们用模拟和理论保证来展示我们的想法的有效性。