On a numerical construction of doubly stochastic matrices with prescribed eigenvalues

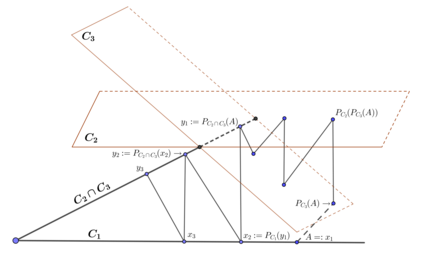
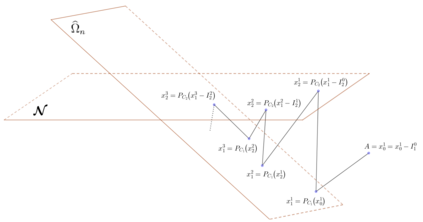
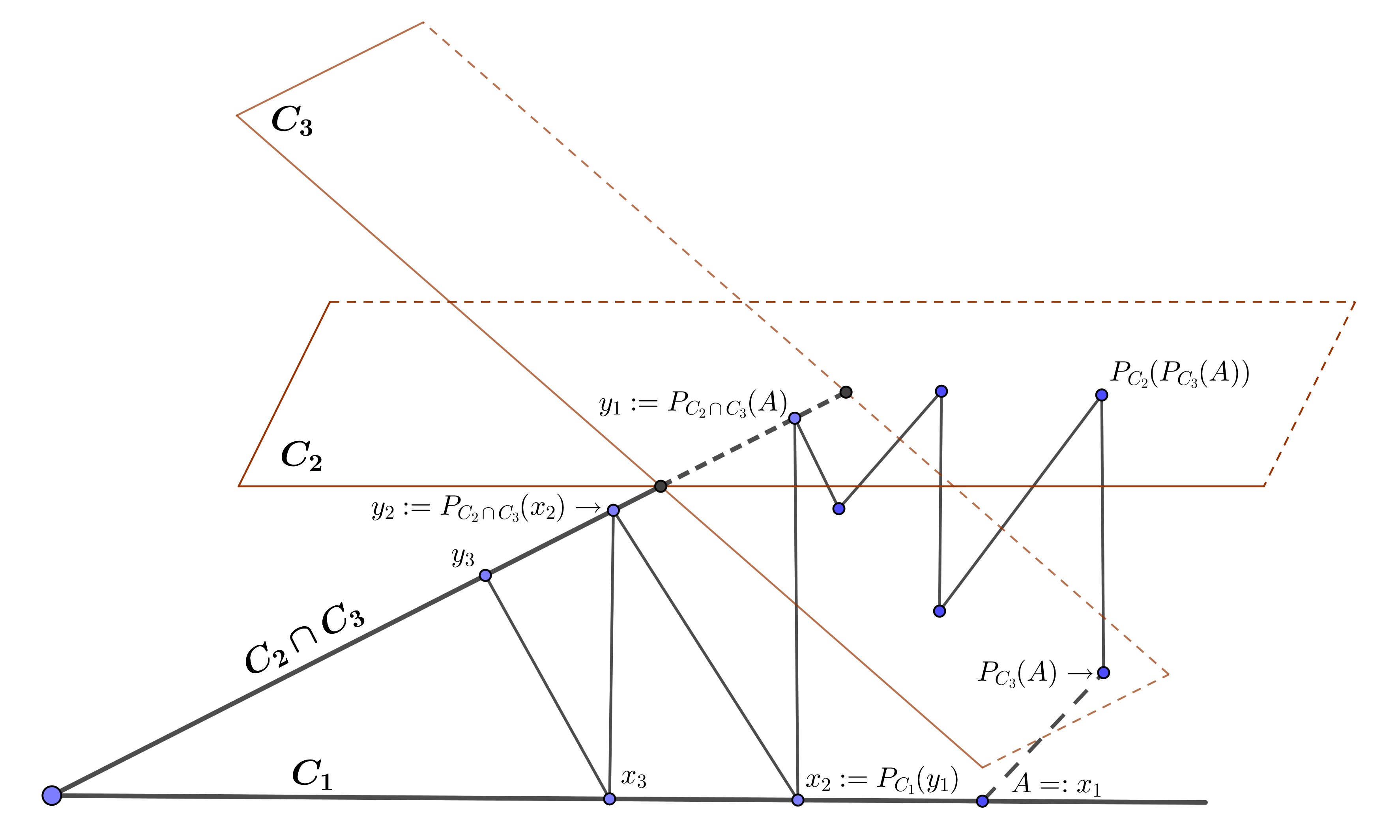
We study the inverse eigenvalue problem for finding doubly stochastic matrices with specified eigenvalues. By making use of a combination of Dykstra's algorithm and an alternating projection process onto a non-convex set, we derive hybrid algorithms for finding doubly stochastic matrices and symmetric doubly stochastic matrices with prescribed eigenvalues. Furthermore, we prove that the proposed algorithms converge and linear convergence is also proved. Numerical examples are presented to demonstrate the efficiency of our method.