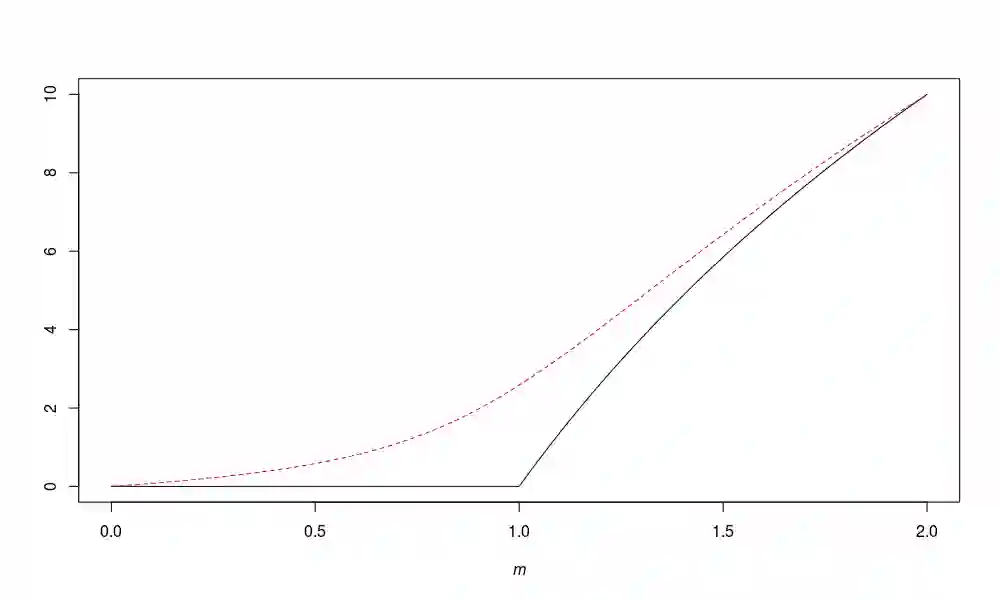
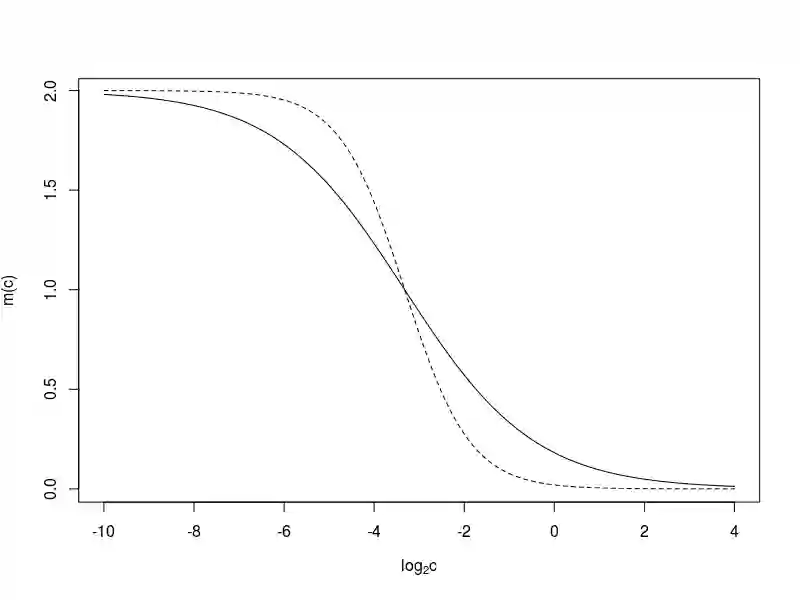
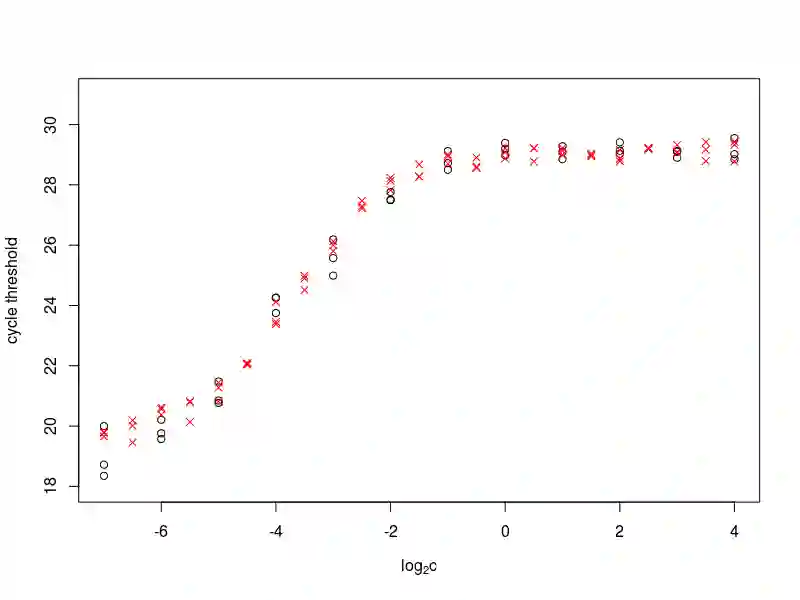
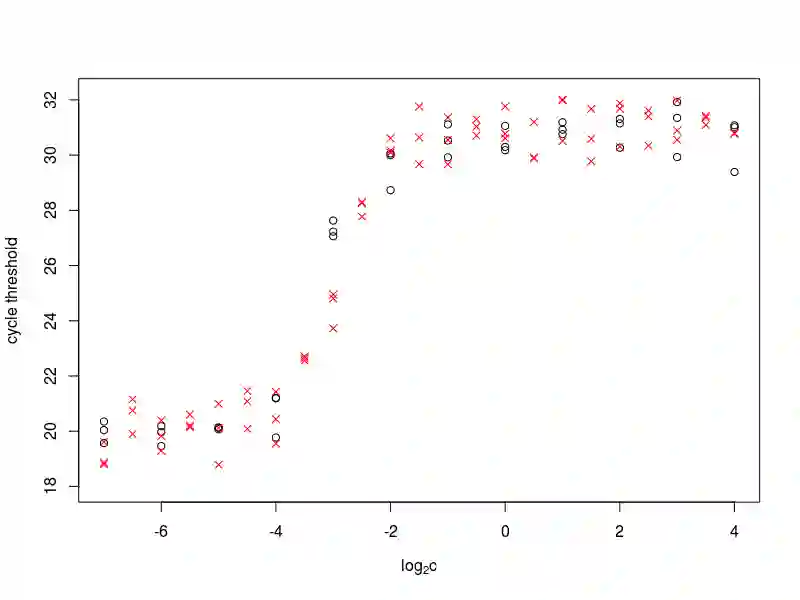
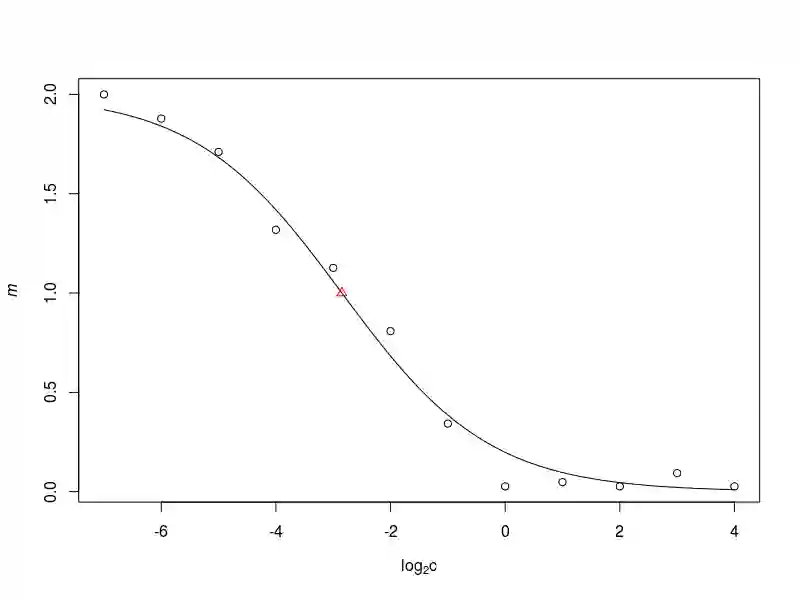
We provide a Galton--Watson model for the growth of a bacterial population in the presence of antibiotics. We assume that bacterial cells either die or duplicate, and the corresponding probabilities depend on the concentration of the antibiotic. Assuming that the mean offspring number is given by $m(c) = 2 / (1 + \alpha c^\beta)$ for some $\alpha, \beta$, where $c$ stands for the antibiotic concentration we obtain weakly consistent, asymptotically normal estimator both for $(\alpha, \beta)$ and for the minimal inhibitory concentration (MIC), a relevant parameter in pharmacology. We apply our method to real data, where \emph{Chlamydia trachomatis} bacteria was treated by azithromycin and ciprofloxacin. For the measurements of \emph{Chlamydia} growth quantitative PCR technique was used. The 2-parameter model fits remarkably well to the biological data.
翻译:我们提供了一种Galton-Watson模型,用于在使用抗生素的情况下增加细菌人口。我们假设细菌细胞要么死亡要么重复,相应的概率取决于抗生素的浓度。假设平均后代数以美元(c) = 2 /(1 + pha c ⁇ beta) 美元给出,其价值大约为 美元(alpha,\ + alpha c ⁇ beta), 美元代表抗生素浓度的微弱一致, 以美元( alpha,\ beta) 和最低抑制性浓度( MIC) 等有关药理学参数计算, 假定平均后代数由美元( cm) = 2 = 2 = 2 = ( 1 + phaltha c ⁇ beta) 美元给出, 以美元表示抗生素浓度, 以美元表示我们获得的抗生素浓度不甚一致的抗体浓度, 以零星正常的正常估计值表示, 以美元表示, 和最低抑制性浓度值( MIC) 和2 参数模型非常适合生物数据。