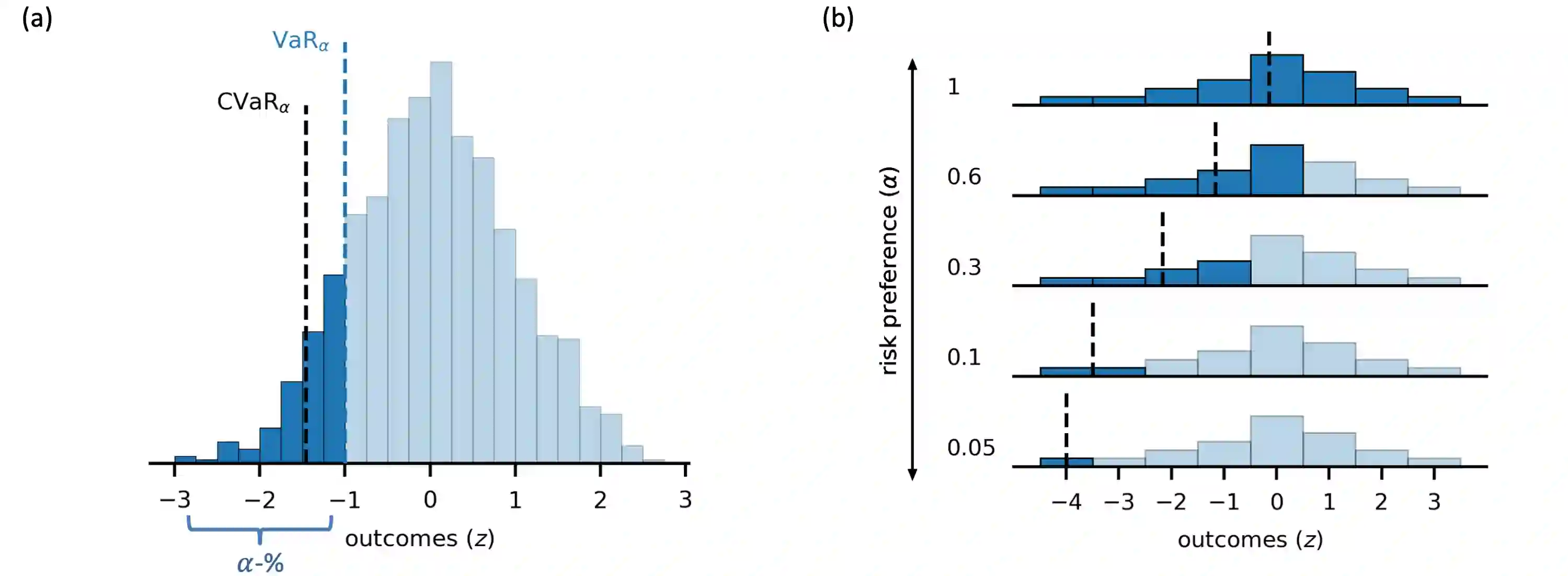
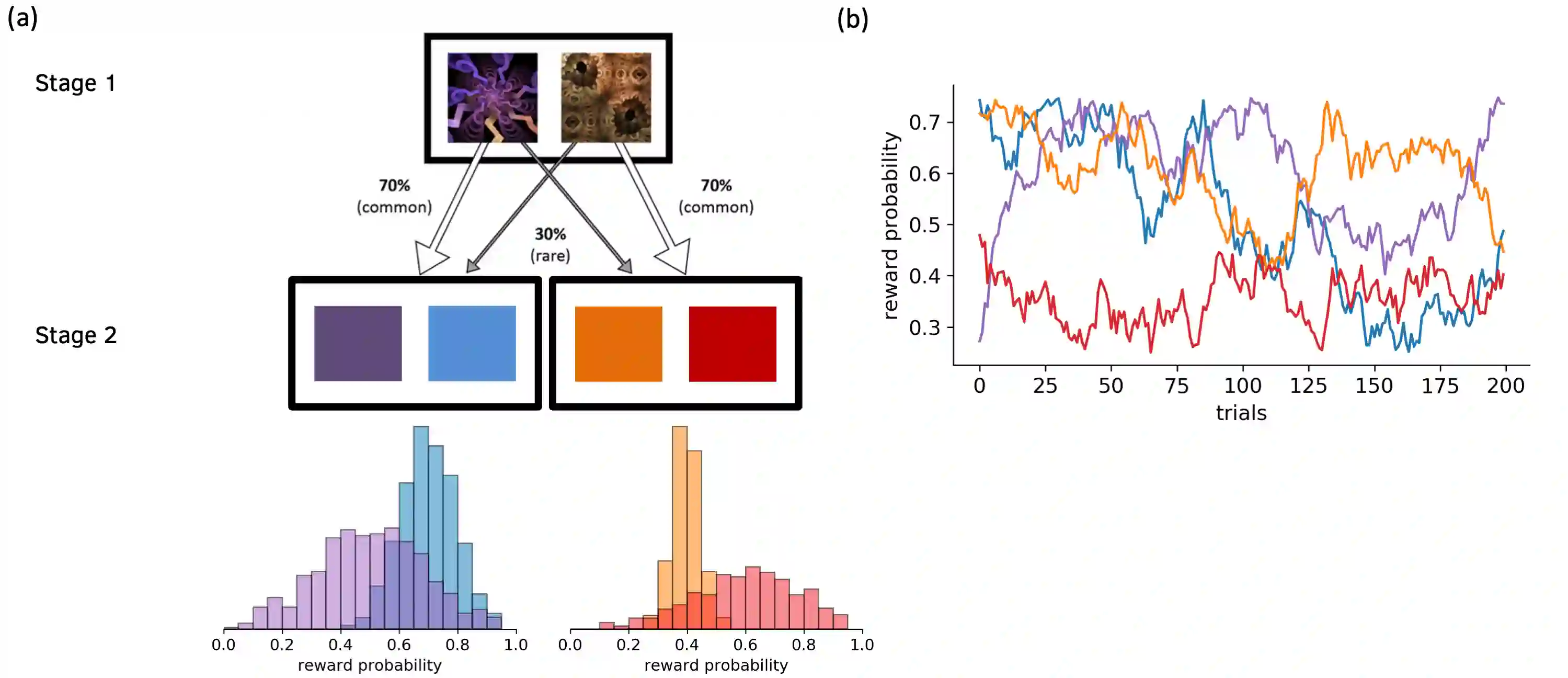
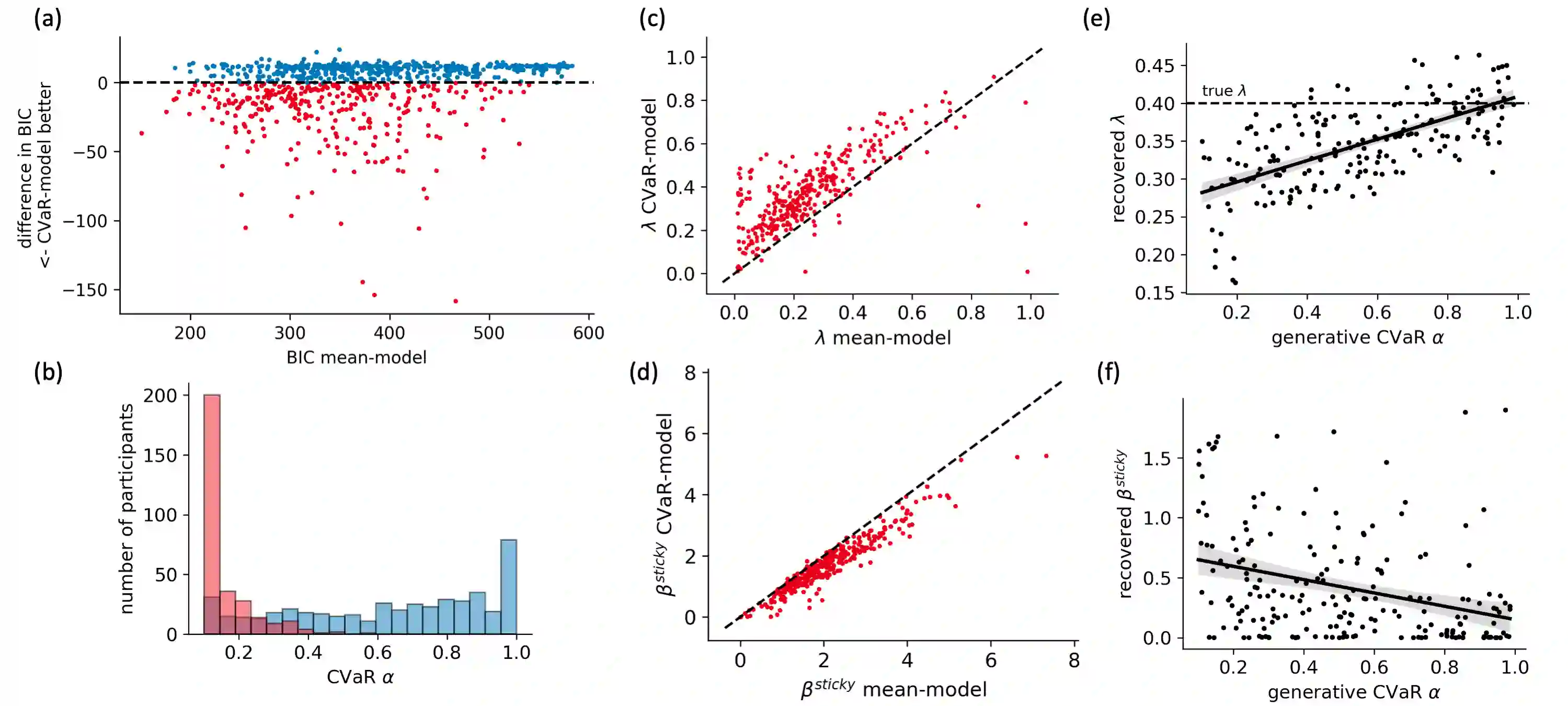
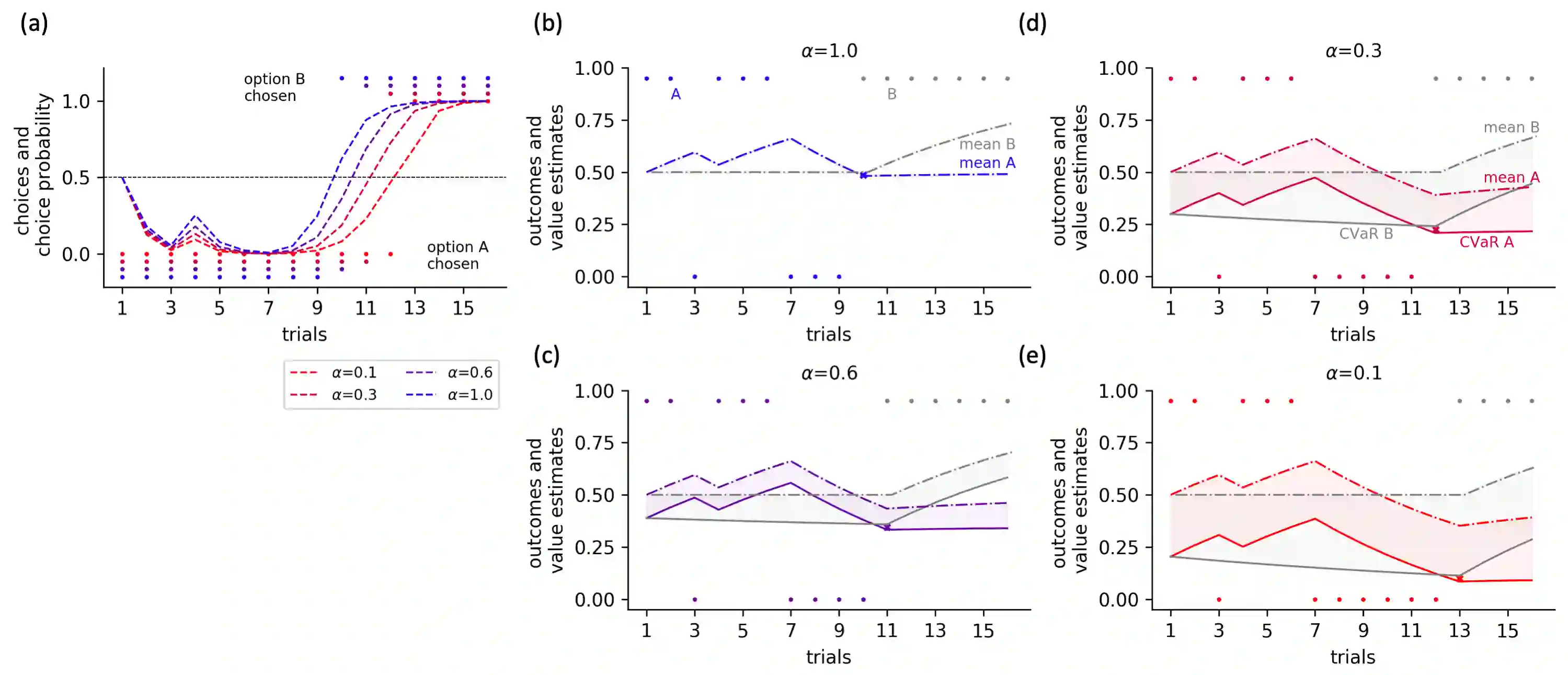
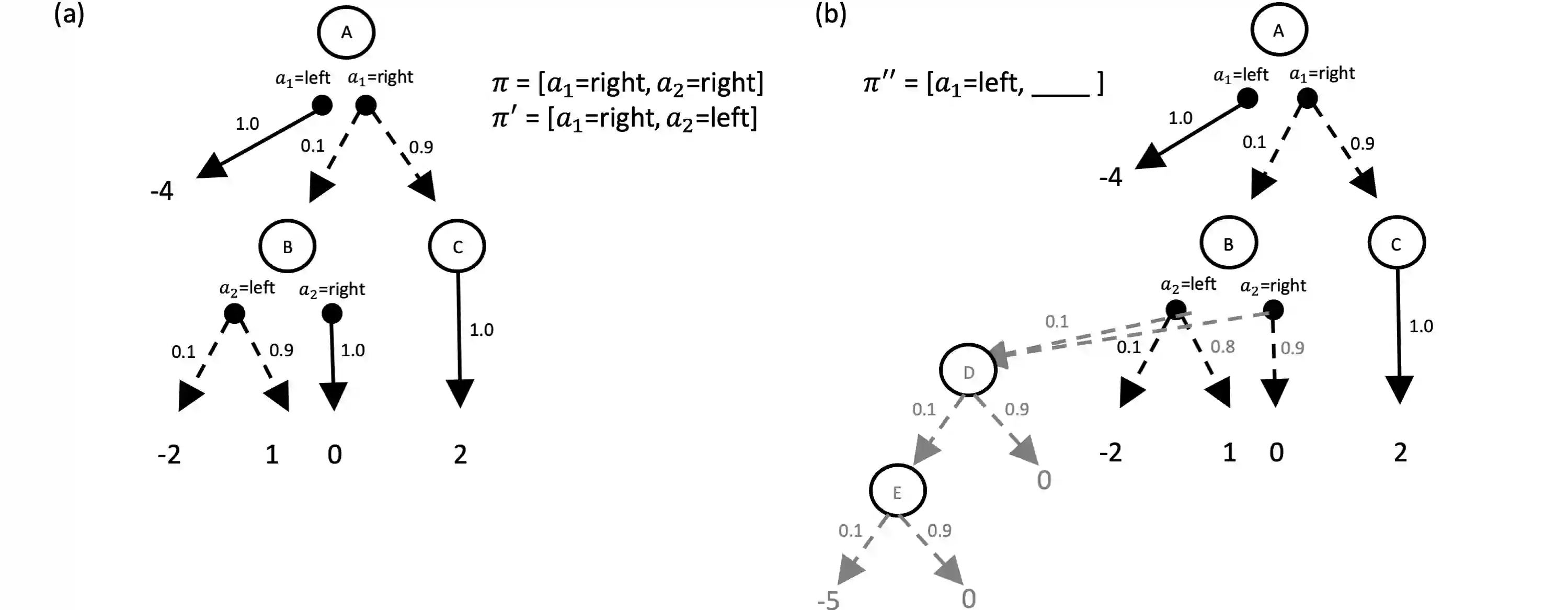
Distributional reinforcement learning (RL) -- in which agents learn about all the possible long-term consequences of their actions, and not just the expected value -- is of great recent interest. One of the most important affordances of a distributional view is facilitating a modern, measured, approach to risk when outcomes are not completely certain. By contrast, psychological and neuroscientific investigations into decision making under risk have utilized a variety of more venerable theoretical models such as prospect theory that lack axiomatically desirable properties such as coherence. Here, we consider a particularly relevant risk measure for modeling human and animal planning, called conditional value-at-risk (CVaR), which quantifies worst-case outcomes (e.g., vehicle accidents or predation). We first adopt a conventional distributional approach to CVaR in a sequential setting and reanalyze the choices of human decision-makers in the well-known two-step task, revealing substantial risk aversion that had been lurking under stickiness and perseveration. We then consider a further critical property of risk sensitivity, namely time consistency, showing alternatives to this form of CVaR that enjoy this desirable characteristic. We use simulations to examine settings in which the various forms differ in ways that have implications for human and animal planning and behavior.
翻译:分配强化学习(RL) -- -- 使代理人了解其行为的所有可能的长期后果,而不仅仅是预期价值 -- -- 在最近引起极大兴趣。分配观点最重要的保障之一是,当结果不完全确定时,促进一种现代的、衡量的、风险的方法。相比之下,对风险决策的心理和神经科学研究利用了各种更可贵的理论模型,例如缺乏一致等同性理想特性的前景理论。在这里,我们考虑了一种特别相关的人类和动物规划模型风险评估措施,称为有条件的值风险(CVAR),它量化了最坏情况的结果(例如,车辆事故或预兆)。我们首先在顺序上对CVaR采取了传统的分配方法,重新分析人类决策者在众所周知的两步任务中的选择,揭示了在粘性与耐性之间潜伏下的重大风险转换。我们随后考虑了一种更关键的风险敏感性特性,即时间一致性,展示了这种方式的替代方法在CVA模型中具有不同形式的模型,我们在这种模型中使用了不同的方式。