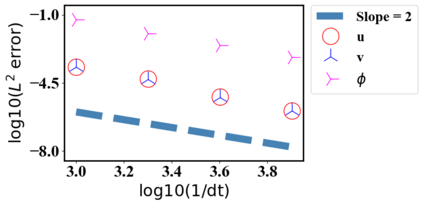
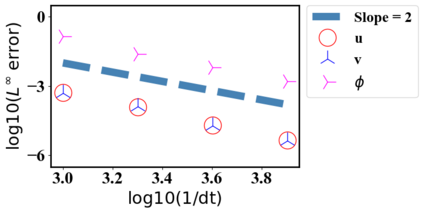
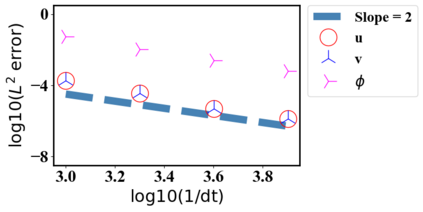
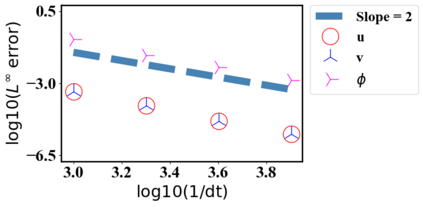
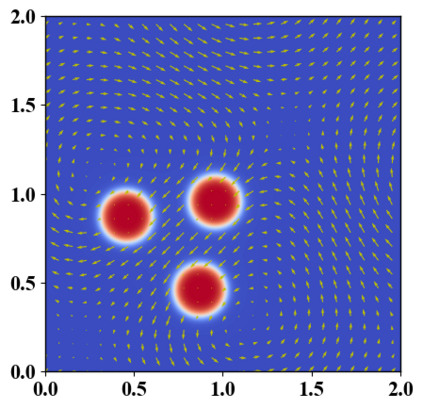
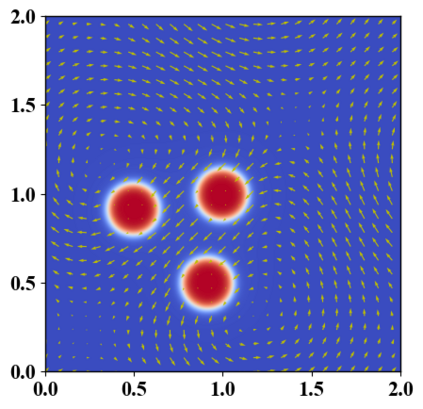
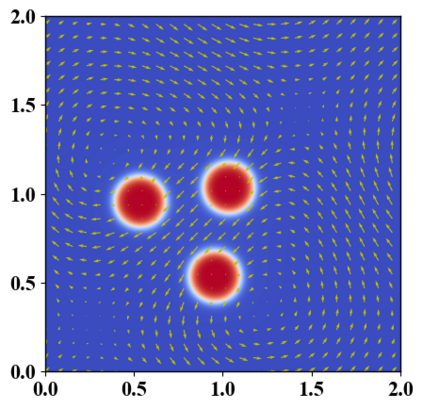
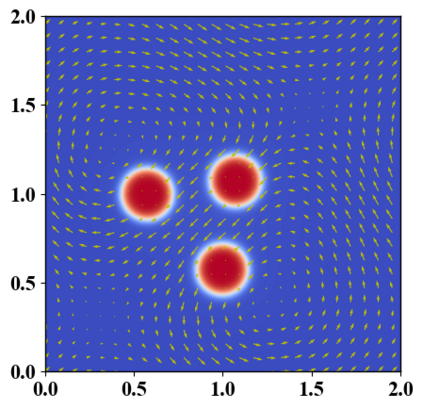
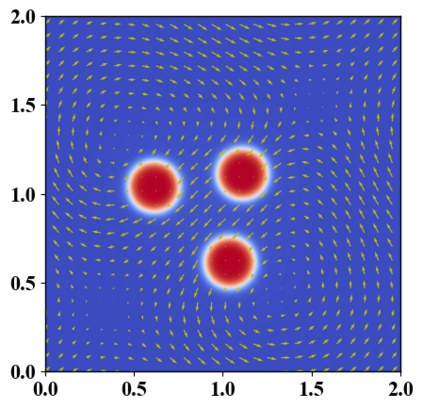
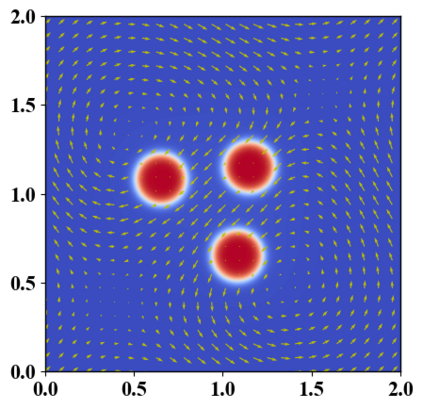
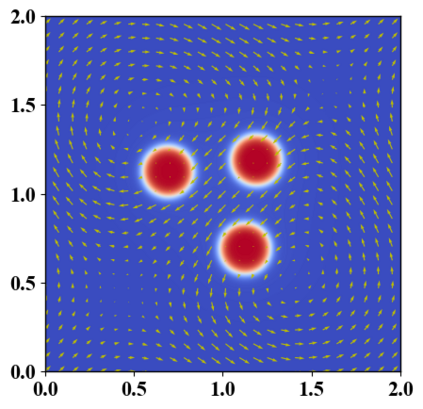
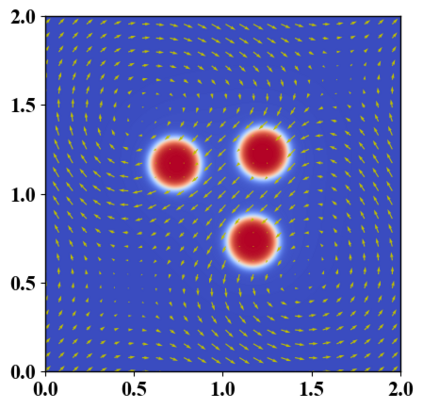
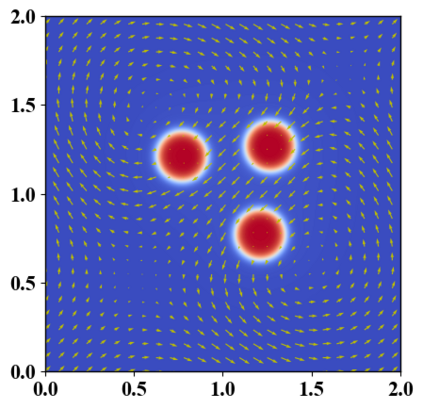
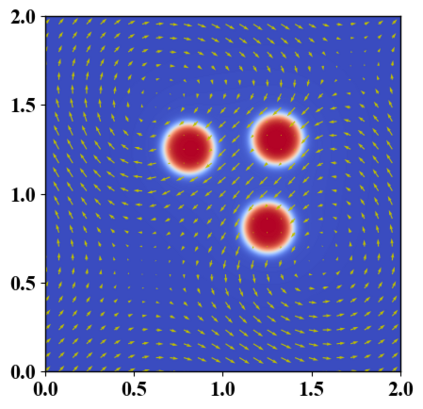
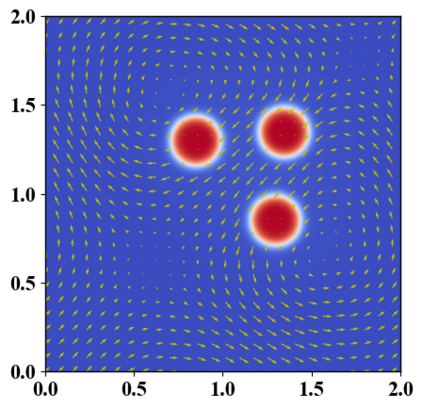
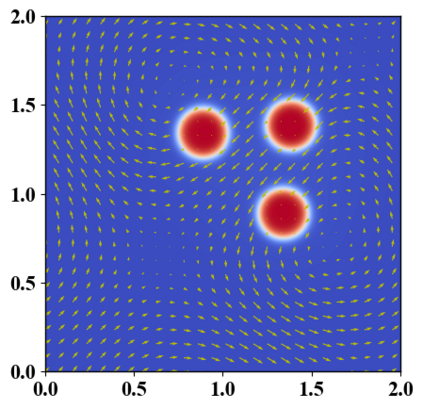
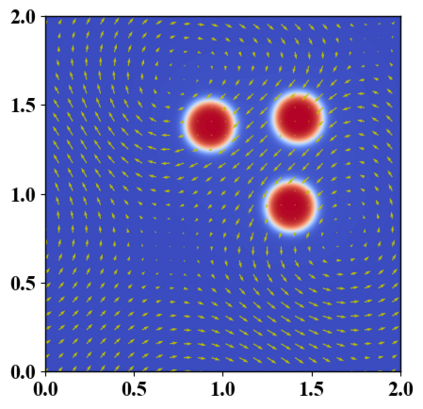
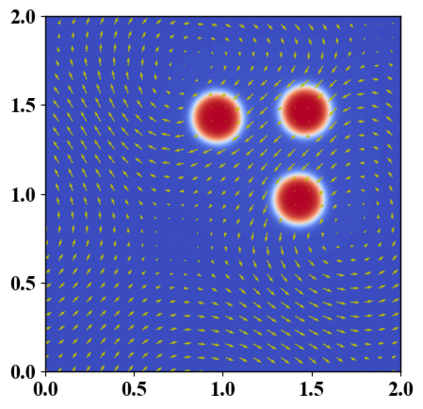
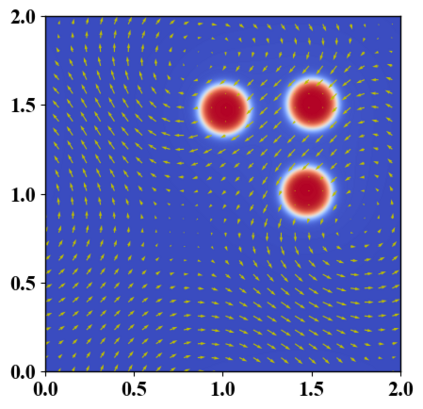
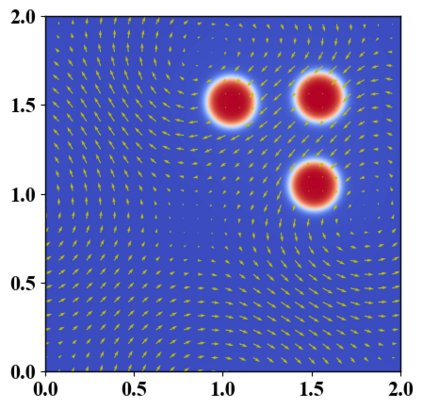
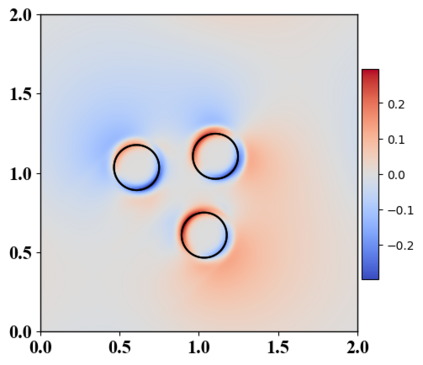
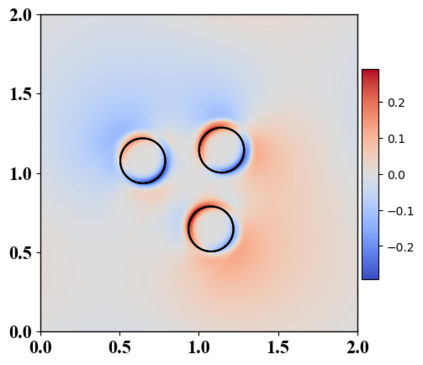
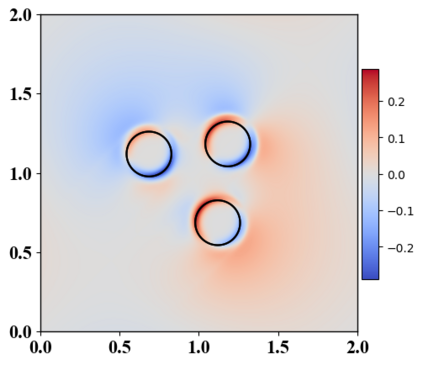
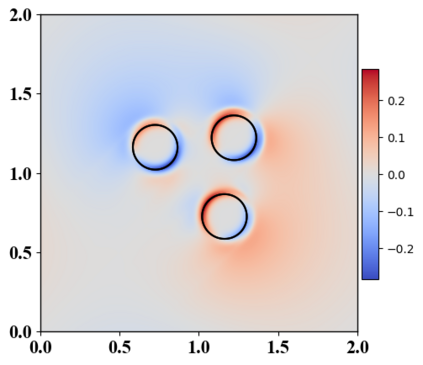
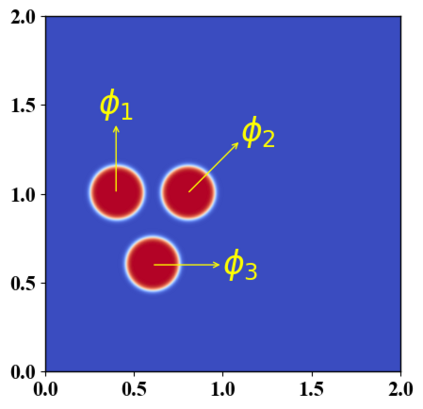
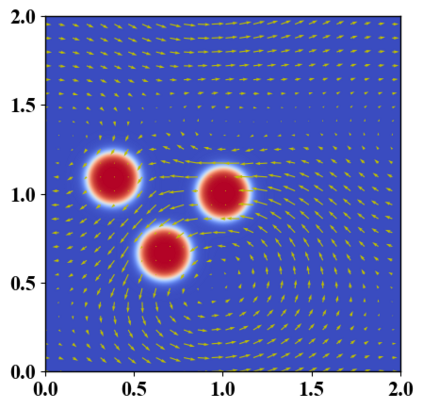
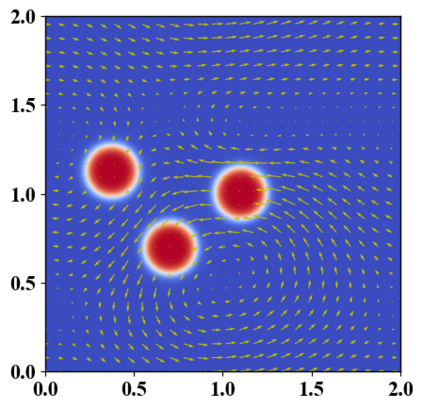
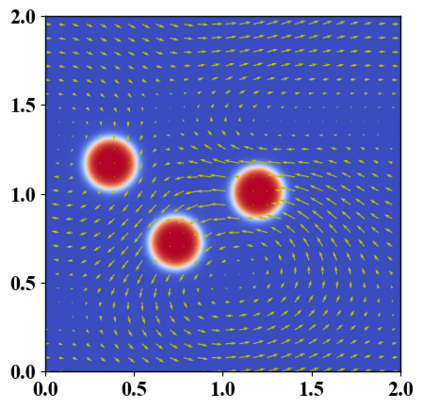
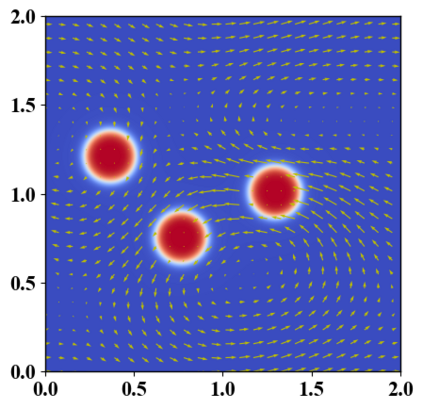
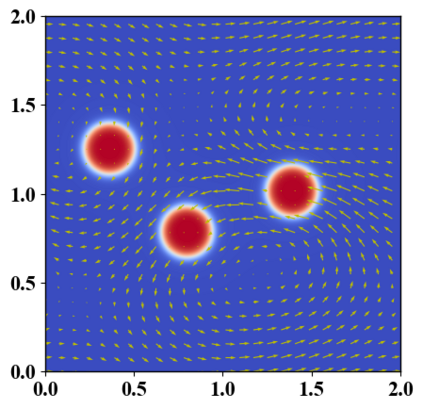
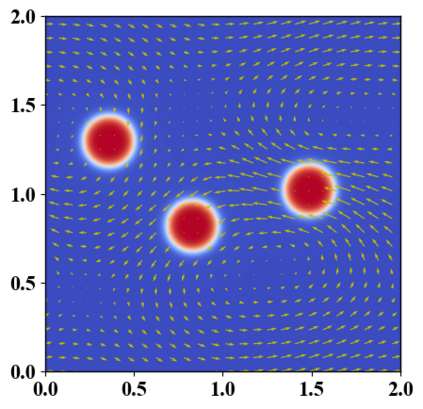
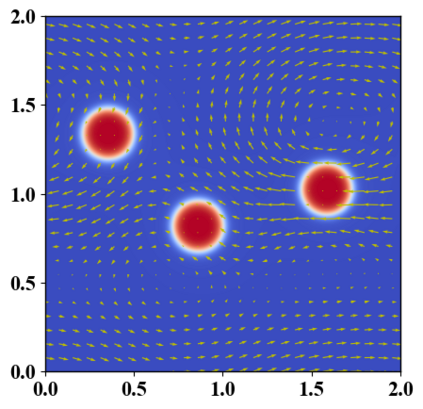
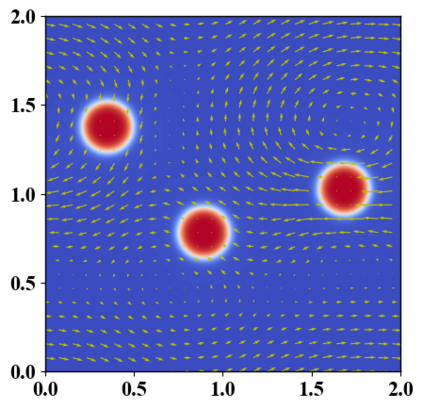
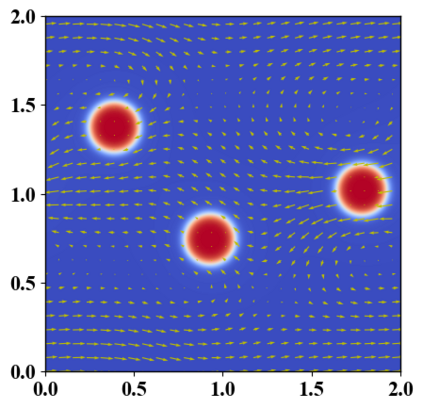
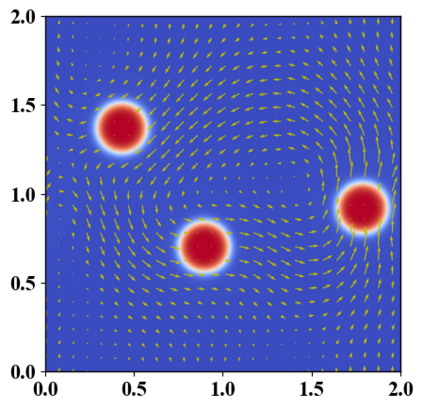
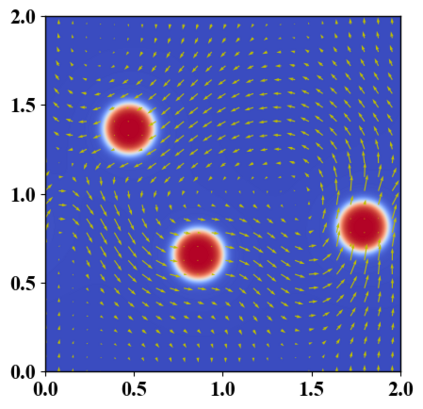
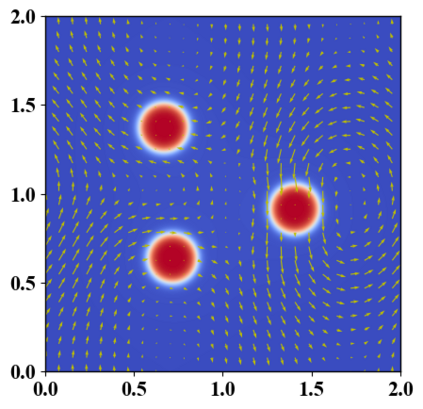
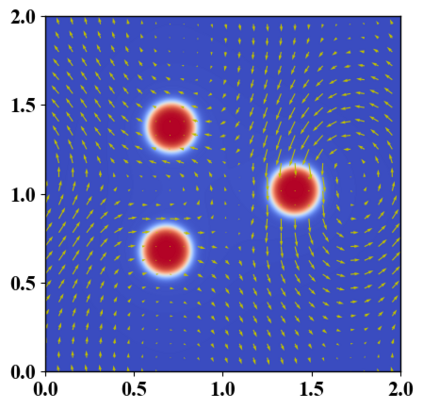
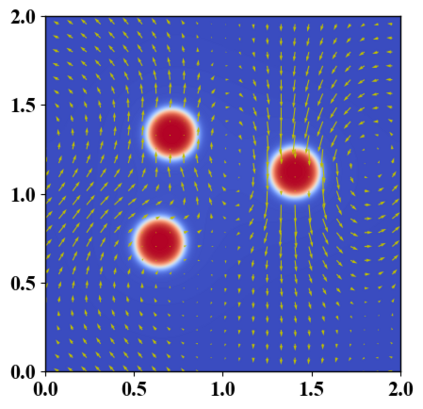
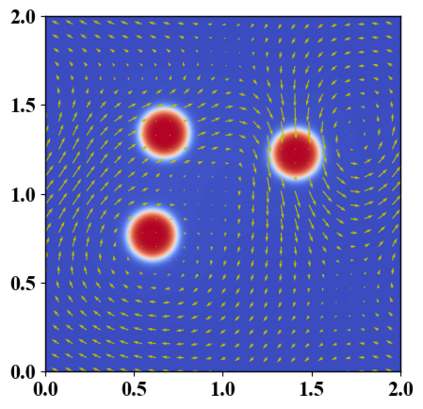
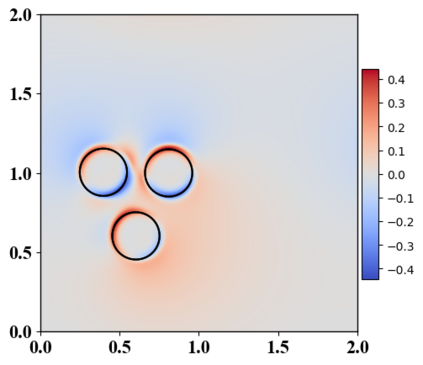
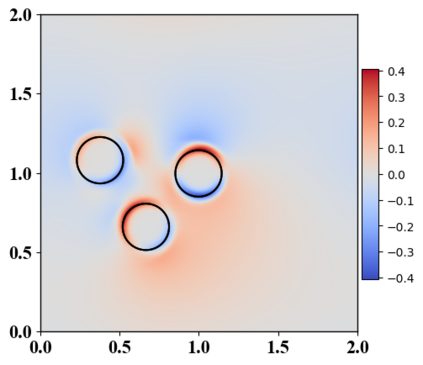
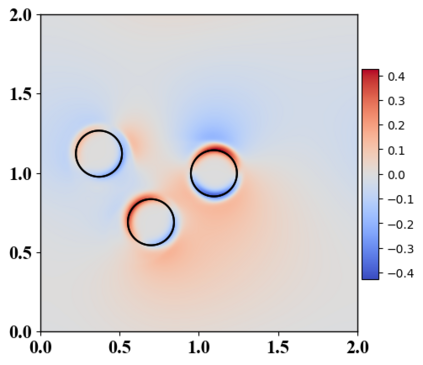
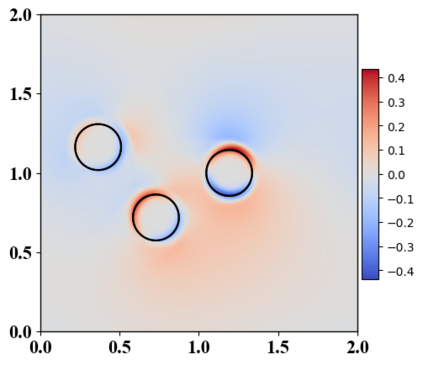
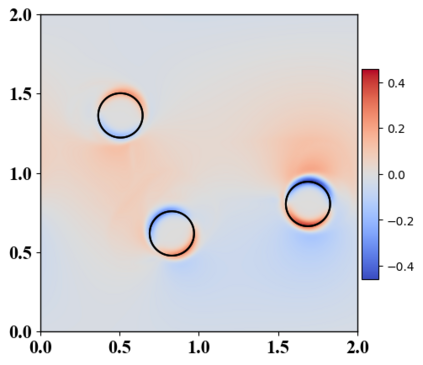
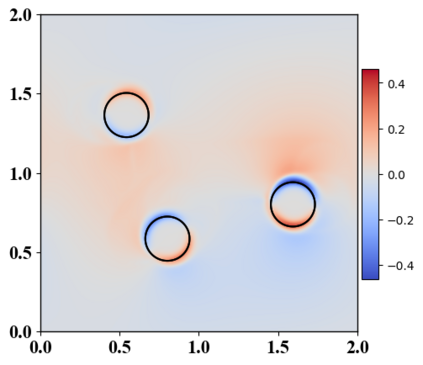
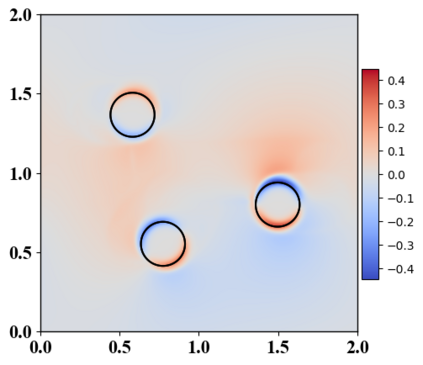
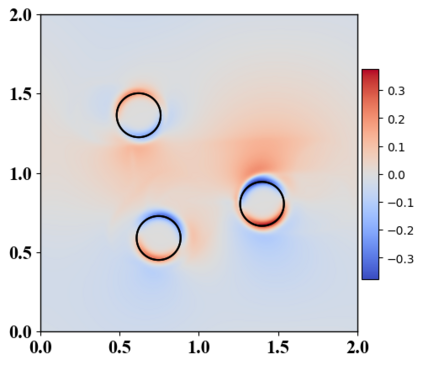
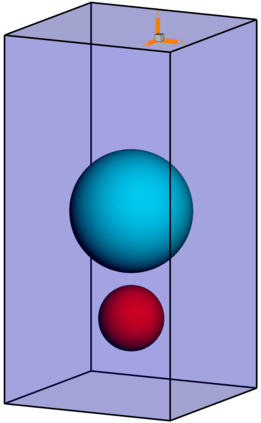
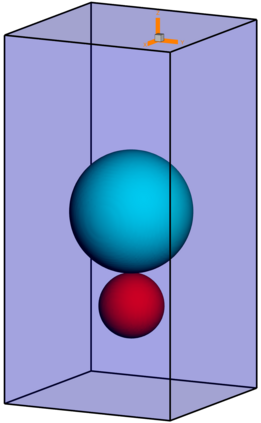
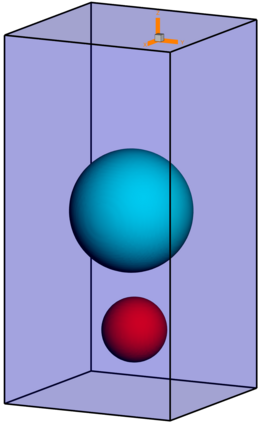
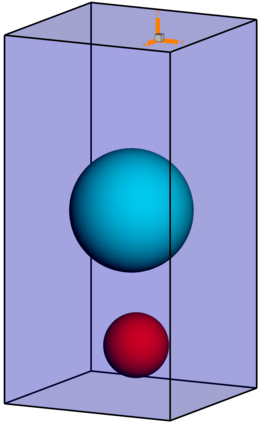
We present a novel computational modeling framework to numerically investigate fluid-structure interaction in viscous fluids using the phase field embedding method. Each rigid body or elastic structure immersed in the incompressible viscous fluid matrix, grossly referred to as the particle in this paper, is identified by a volume preserving phase field. The motion of the particle is driven by the fluid velocity in the matrix for passive particles or combined with its self-propelling velocity for active particles. The excluded volume effect between a pair of particles or between a particle and the boundary is modeled by a repulsive potential force. The drag exerted to the fluid by a particle is assumed proportional to its velocity. When the particle is rigid, its state is described by a zero velocity gradient tensor within the nonzero phase field that defines its profile and a constraining stress exists therein. While the particle is elastic, a linear constitutive equation for the elastic stress is provided within the particle domain. A hybrid, thermodynamically consistent hydrodynamic model valid in the entire computational domain is then derived for the fluid-particle ensemble using the generalized Onsager principle accounting for both rigid and elastic particles. Structure-preserving numerical algorithms are subsequently developed for the thermodynamically consistent model. Numerical tests in 2D and 3D space are carried out to verify the rate of convergence and numerical examples are given to demonstrate the usefulness of the computational framework for simulating fluid-structure interactions for passive as well as self-propelling active particles in a viscous fluid matrix.
翻译:我们提出了一个新的计算模型框架,用于利用相向嵌入法对粘结液中的流体结构相互作用进行数值调查。 被本文中粗略称为粒子的不可压缩的粘结状体或弹性结构, 由量保存相字段来识别。 粒子的运动是由被动粒子矩阵中的流体速度驱动的, 或与其对活性粒子的自我推进速度相结合的。 粒子之间或粒子与边界之间的排除体积效应, 由可令人反感的潜在力量来模拟。 粒子对流体的拖动或弹性结构, 假定与它的速度成比例。 当粒子为僵硬时, 其状态被以非零速度缩压粒子字段中的零速度梯度推导出。 虽然粒子是弹性粒子矩阵中的流体速度速度, 弹性微量压力的线性组合在粒子域内提供。 在整个计算域中有效的混合、 恒流体动态流体流体动力流体动力动力模型, 然后为流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 主动性- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体-, 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体- 流体-