Mapping the intensity function of a non-stationary point process in unobserved areas

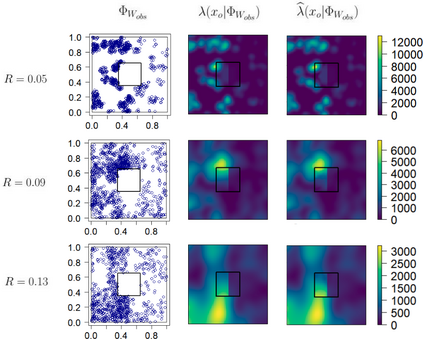
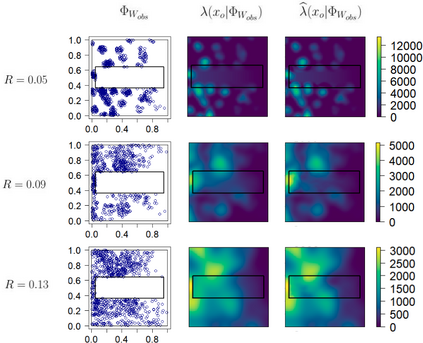
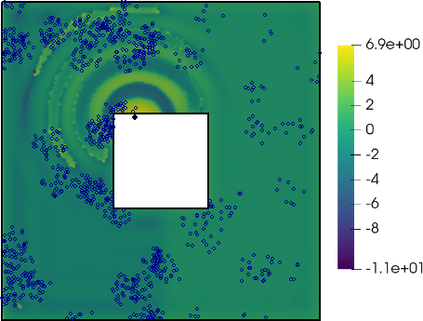
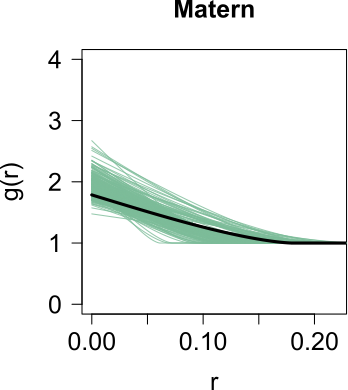
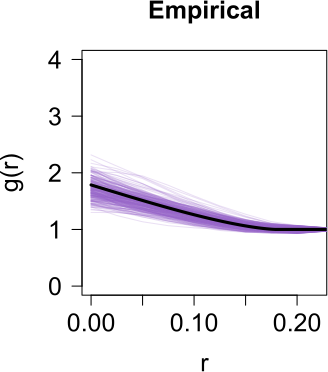
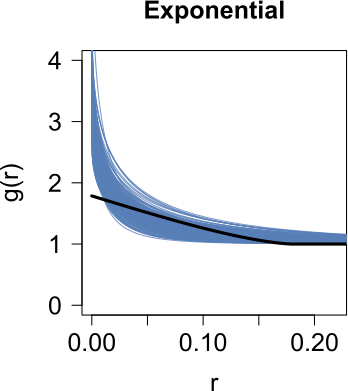
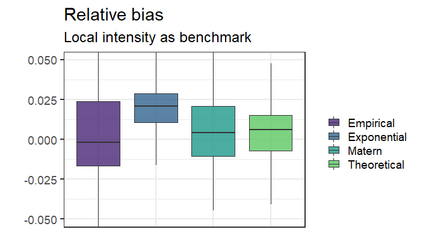
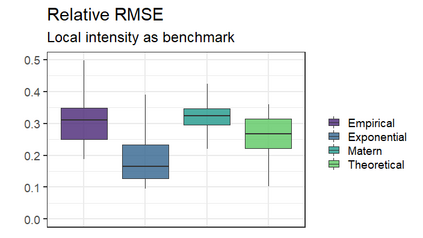
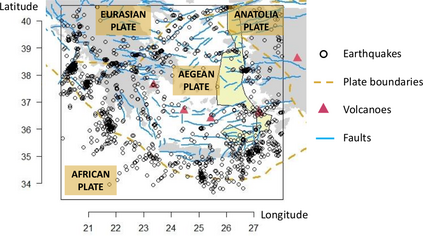
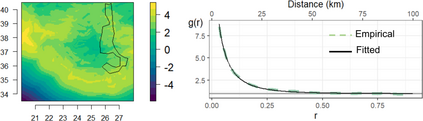
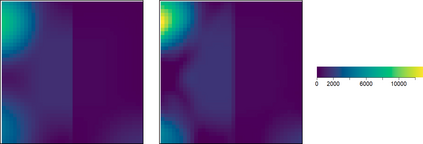
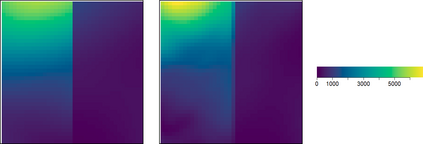
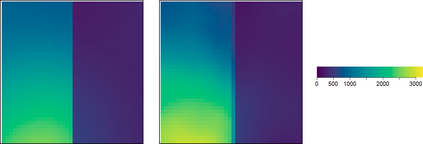
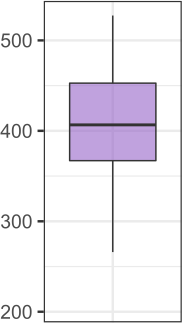
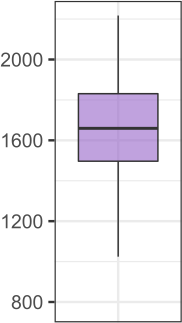
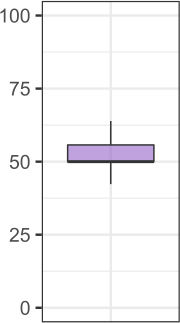
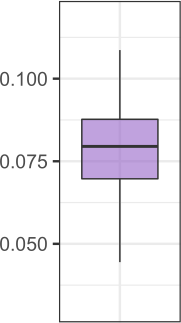
Seismic networks provide data that are used as basis both for public safety decisions and for scientific research. Their configuration affects the data completeness, which in turn, critically affects several seismological scientific targets (e.g., earthquake prediction, seismic hazard...). In this context, a key aspect is how to map earthquakes density in seismogenic areas from censored data or even in areas that are not covered by the network. We propose to predict the spatial distribution of earthquakes from the knowledge of presence locations and geological relationships, taking into account any interaction between records. Namely, in a more general setting, we aim to estimate the intensity function of a point process, conditional to its censored realization, as in geostatistics for continuous processes. We define a predictor as the best linear unbiased combination of the observed point pattern. We show that the weight function associated to the predictor is the solution of a Fredholm equation of second kind. Both the kernel and the source term of the Fredholm equation are related to the first-and second-order characteristics of the point process through the intensity and the pair correlation function. Results are presented and illustrated on simulated non-stationary point processes and real data for mapping Greek Hellenic seismicity in a region with unreliable and incomplete records.