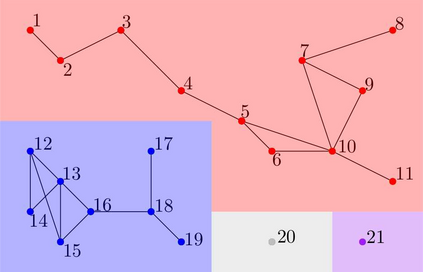
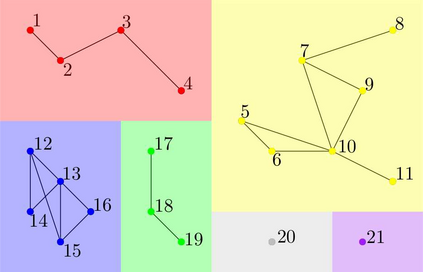
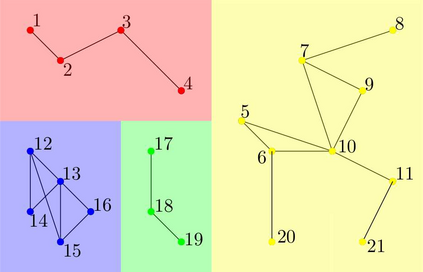
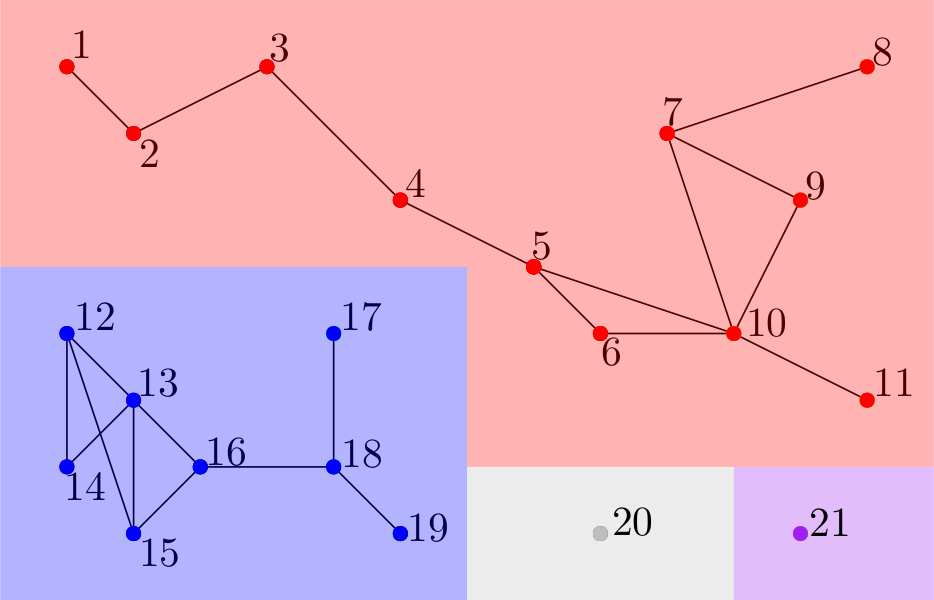
We propose a novel infection spread model based on a random connection graph which represents connections between $n$ individuals. Infection spreads via connections between individuals and this results in a probabilistic cluster formation structure as well as a non-i.i.d. (correlated) infection status for individuals. We propose a class of two-step sampled group testing algorithms where we exploit the known probabilistic infection spread model. We investigate the metrics associated with two-step sampled group testing algorithms. To demonstrate our results, for analytically tractable exponentially split cluster formation trees, we calculate the required number of tests and the expected number of false classifications in terms of the system parameters, and identify the trade-off between them. For such exponentially split cluster formation trees, for zero-error construction, we prove that the required number of tests is $O(\log_2n)$. Thus, for such cluster formation trees, our algorithm outperforms any zero-error non-adaptive group test, binary splitting algorithm, and Hwang's generalized binary splitting algorithm. Our results imply that, by exploiting probabilistic information on the connections of individuals, group testing can be used to reduce the number of required tests significantly even when infection rate is high, contrasting the prevalent belief that group testing is useful only when infection rate is low.
翻译:我们建议基于随机连接图的新型感染传播模式,该模式代表了个人与美元之间的连接。 感染通过个人之间的连接扩散,这导致个人形成一个概率性的集群形成结构以及非i.i.d.(与气候有关)感染状态。 我们建议了一组两步抽样群体测试算法,在那里我们利用已知的概率性感染传播模式。 我们调查了与两步抽样群体测试算法相关的衡量标准。 为了展示我们的结果,在分析上可移动的指数分解集群形成树上,我们计算了所需的测试数量和系统参数参数方面错误分类的预期数量,并确定了两者之间的交易。 对于这种指数性分裂的集群形成树,我们建议了一组零度构造,我们证明所需的测试数量是$(\log_2n)$。 因此,对于这些集群形成型树,我们的算法超过了任何零性不适应性群体测试的尺度。 对于可分析性指数分解算法和黄氏通用的分解算法,我们计算结果表明,在系统参数参数方面所需的测试数量,以及他们之间的交易。 对于这种突变现式组合来说,我们的结果意味着,在利用高度测试时,在使用高度的感染率测试时, 测试时,只有对低感染率的对个人的测试,只有对低比例的测试,我们所使用的集体的判断,只有对低比例的判断,只有对低的测试才能降低式测试,只有对低的测试。