Advice Complexity of Online Non-Crossing Matching

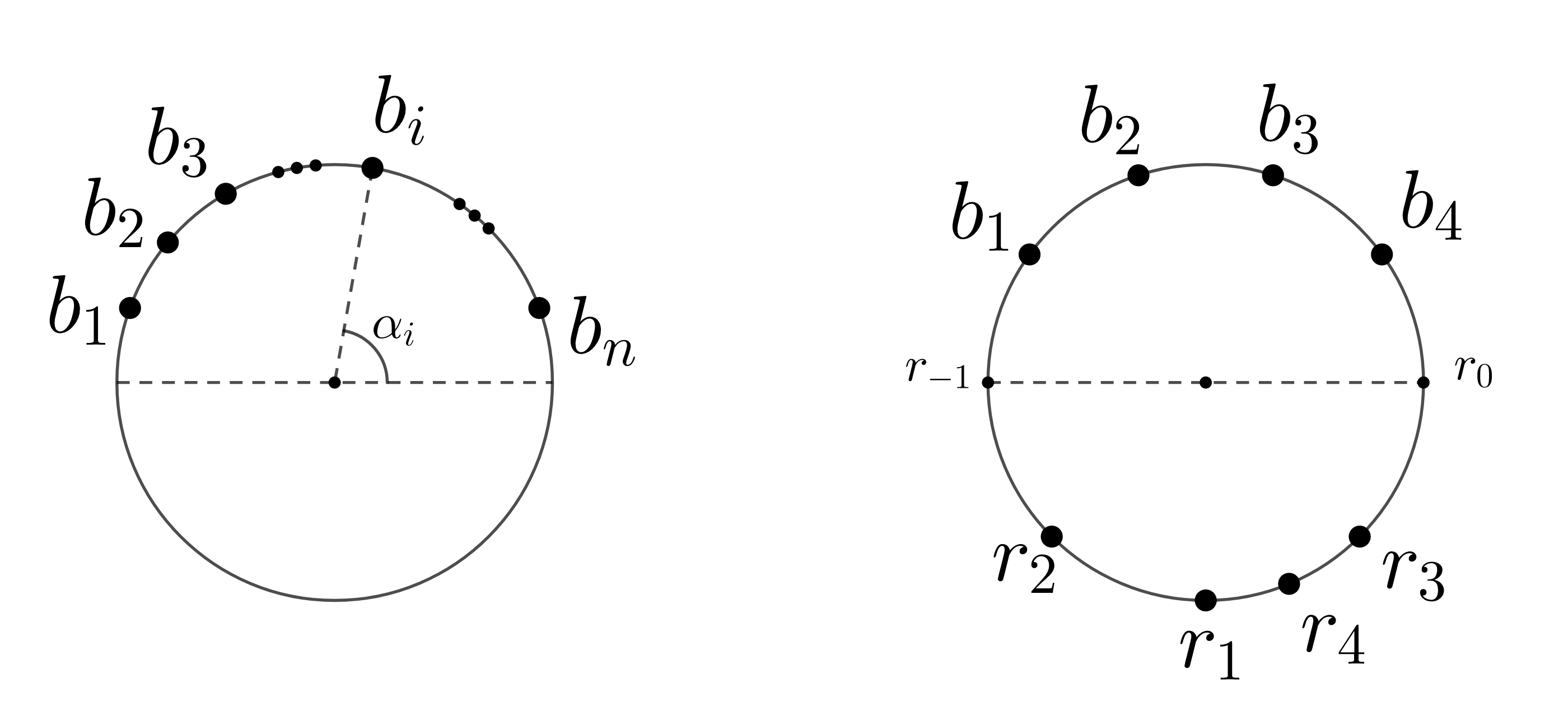
We study online matching in the Euclidean $2$-dimesional plane with non-crossing constraint. The offline version was introduced by Atallah in 1985 and the online version was introduced and studied more recently by Bose et al. The input to the problem consists of a sequence of points, and upon arrival of a point an algorithm can match it with a previously unmatched point provided that line segments corresponding to the matched edges do not intersect. The decisions are irrevocable, and while an optimal offline solution always matches all the points, an online algorithm cannot match all the points in the worst case, unless it is given some side information, i.e., advice. We study two versions of this problem -- monomchromatic (MNM) and bichromatic (BNM). We show that advice complexity of solving BNM optimally on a circle (or, more generally, on inputs in a convex position) is tightly bounded by the logarithm of the $n^\text{th}$ Catalan number from above and below. This result corrects the previous claim of Bose et al. that the advice complexity is $\log(n!)$. At the heart of the result is a connection between non-crossing constraint in online inputs and $231$-avoiding property of permutations of $n$ elements We also show a lower bound of $n/3-1$ and an upper bound of $3n$ on the advice complexity for MNM on a plane. This gives an exponential improvement over the previously best known lower bound and an improvement in the constant of the leading term in the upper bound. In addition, we establish a lower bound of $\frac{\alpha}{2}\infdiv{\frac{2(1-\alpha)}{\alpha}}{1/4}n$ on the advice complexity for achieving competitive ratio $\alpha$ for MNM on a circle. Standard tools from advice complexity, such as partition trees and reductions from string guessing problem, do not seem to apply to MNM/BNM, so we have to design our lower bounds from first principles.