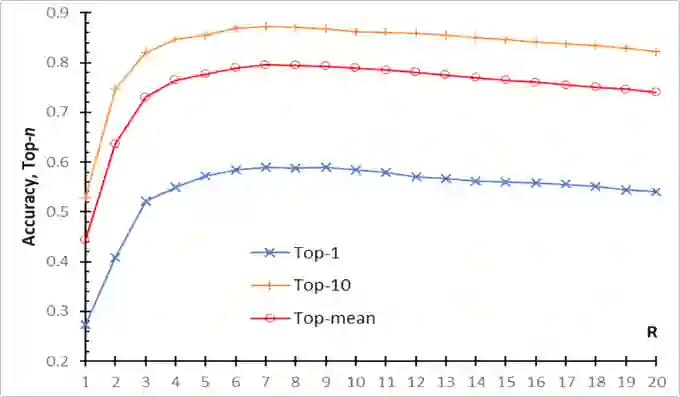
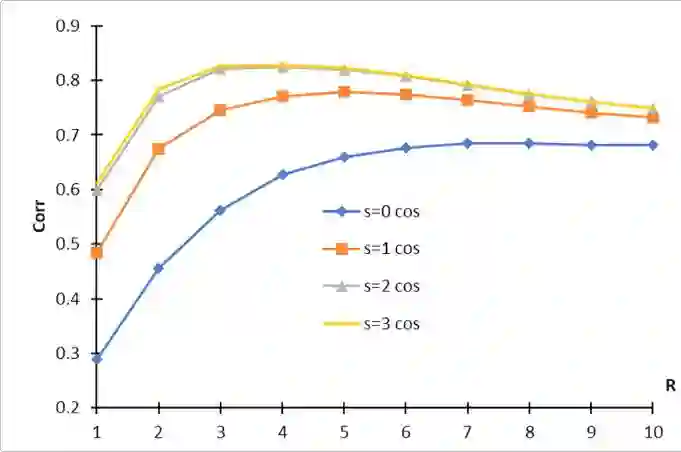
Hyperdimensional Computing (HDC), also known as Vector-Symbolic Architectures (VSA), is a promising framework for the development of cognitive architectures and artificial intelligence systems, as well as for technical applications and emerging neuromorphic and nanoscale hardware. HDC/VSA operate with hypervectors, i.e., distributed vector representations of large fixed dimension (usually > 1000). One of the key ingredients of HDC/VSA are the methods for encoding data of various types (from numeric scalars and vectors to graphs) into hypervectors. In this paper, we propose an approach for the formation of hypervectors of sequences that provides both an equivariance with respect to the shift of sequences and preserves the similarity of sequences with identical elements at nearby positions. Our methods represent the sequence elements by compositional hypervectors and exploit permutations of hypervectors for representing the order of sequence elements. We experimentally explored the proposed representations using a diverse set of tasks with data in the form of symbolic strings. Although our approach is feature-free as it forms the hypervector of a sequence from the hypervectors of its symbols at their positions, it demonstrated the performance on a par with the methods that apply various features, such as subsequences. The proposed techniques were designed for the HDC/VSA model known as Sparse Binary Distributed Representations. However, they can be adapted to hypervectors in formats of other HDC/VSA models, as well as for representing sequences of types other than symbolic strings.
翻译:HDC/VSA使用高压摄像器操作。HDC/VSA的主要成份之一是将各种类型数据(从数值标度和矢量到图表)编码为超常量数据的方法。在本文件中,我们提出了一种方法,用于构建各种认知结构和人工智能系统,以及技术应用和新兴神经畸形和纳米级硬件。HDC/VSA使用高压摄像器操作。HDC/VSA使用高压矢量表示大固定尺寸(通常大于1000)的分布式矢量表示。HDC/VSA的主要成份之一是将各种类型的数据(从数字标度和矢量到图表)编码成超强量值数据。在本文中,我们提出了一种方法,用于构建高压结构的超量变量和超量序列,同时我们的方法在顺序的顺序中提供了一种不偏差的质的比值格式,在高频度模型中,在高频度代表了高分辨率标度方的多位数结构中,在高压层代表了高压级方方位数的动作中,在高压结构中展示了它作为多质的多层次的演算法。