Deep energy method in topology optimization applications

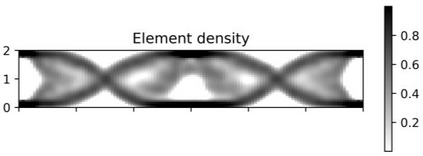
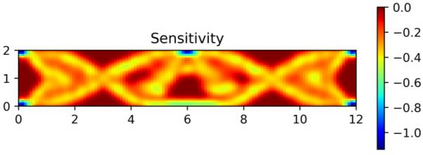
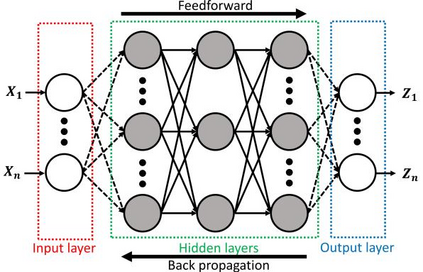
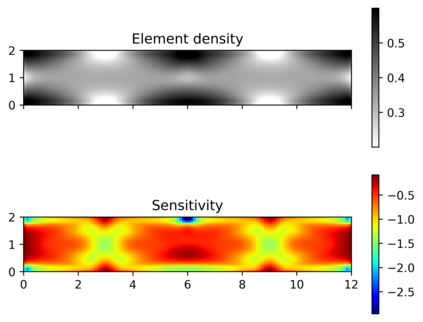
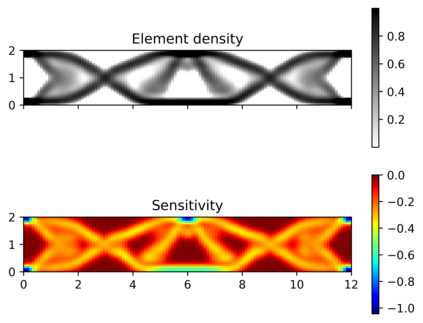
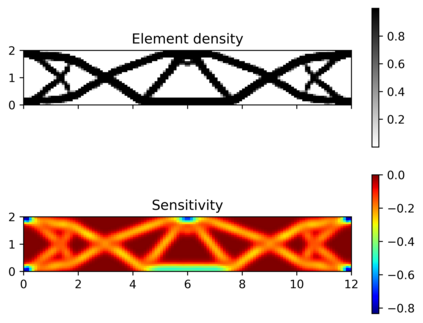
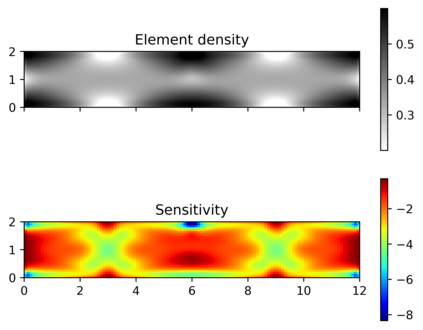
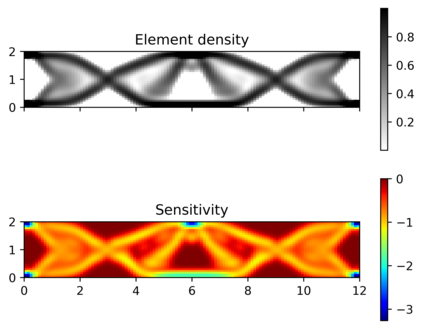
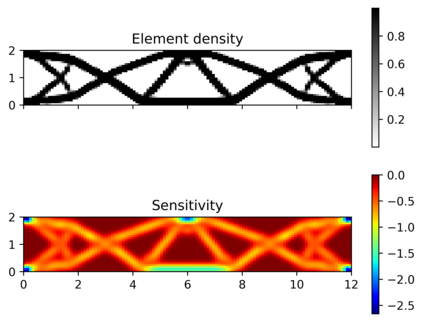
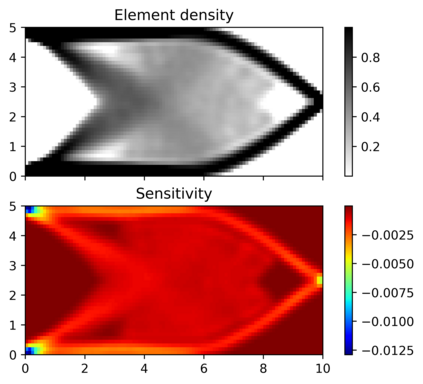
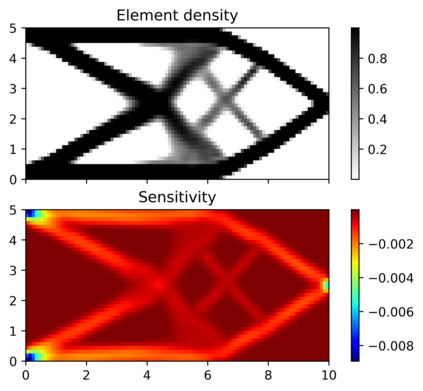
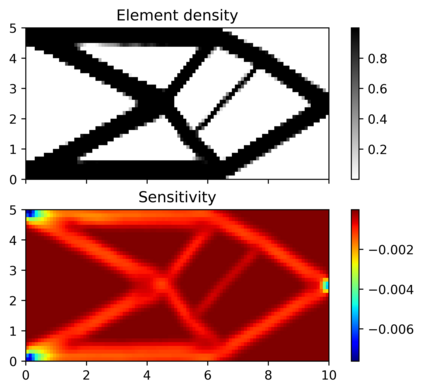
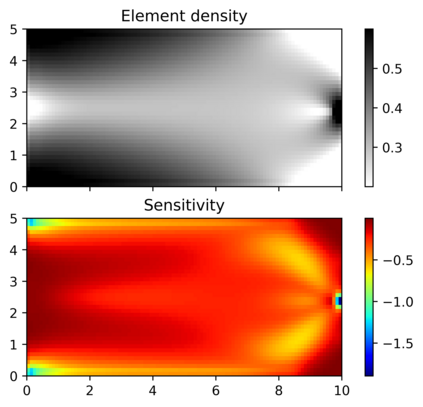
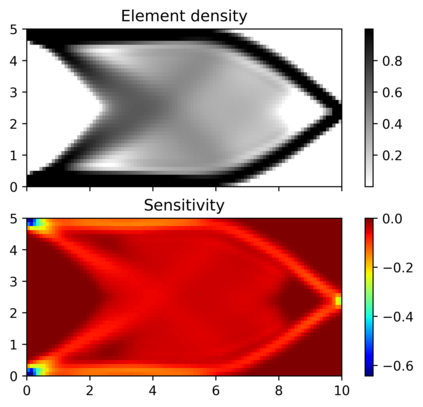
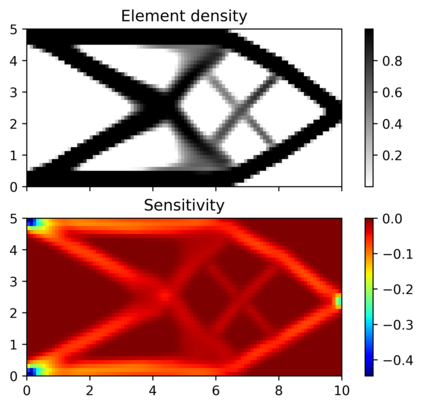
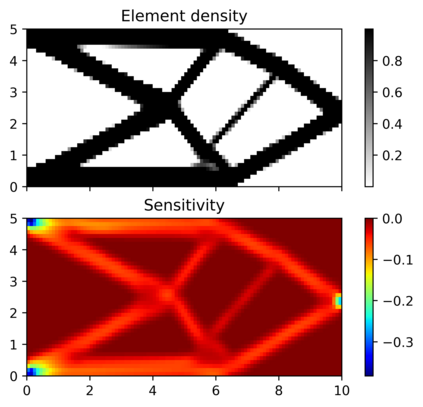
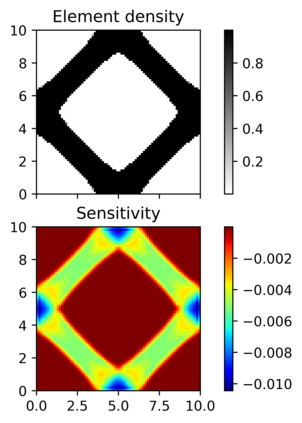
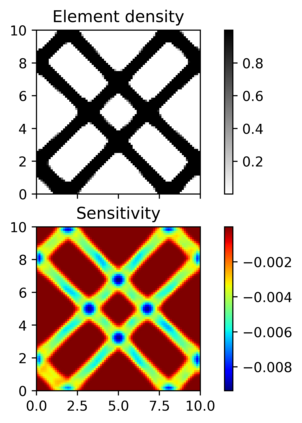
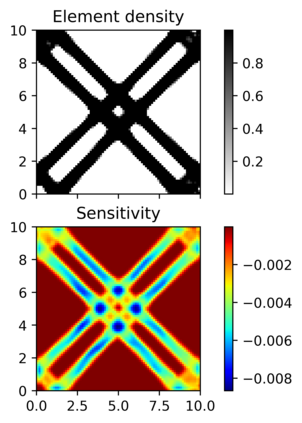
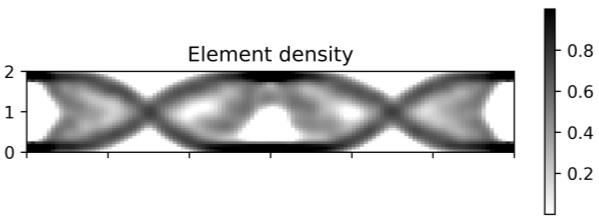
This paper explores the possibilities of applying physics-informed neural networks (PINNs) in topology optimization (TO) by introducing a fully self-supervised TO framework that is based on PINNs. This framework solves the forward elasticity problem by the deep energy method (DEM). Instead of training a separate neural network to update the density distribution, we leverage the fact that the compliance minimization problem is self-adjoint to express the element sensitivity directly in terms of the displacement field from the DEM model, and thus no additional neural network is needed for the inverse problem. The method of moving asymptotes is used as the optimizer for updating density distribution. The implementation of Neumann, Dirichlet, and periodic boundary conditions are described in the context of the DEM model. Three numerical examples are presented to demonstrate framework capabilities: (1) Compliance minimization in 2D under different geometries and loading, (2) Compliance minimization in 3D, and (3) Maximization of homogenized shear modulus to design 2D meta material unit cells. The results show that the optimized designs from the DEM-based framework are very comparable to those generated by the finite element method, and shed light on a new way of integrating PINN-based simulation methods into classical computational mechanics problems.