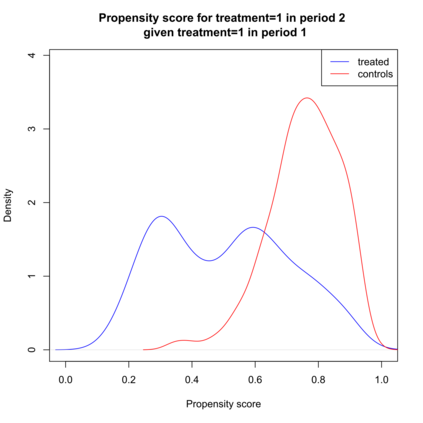
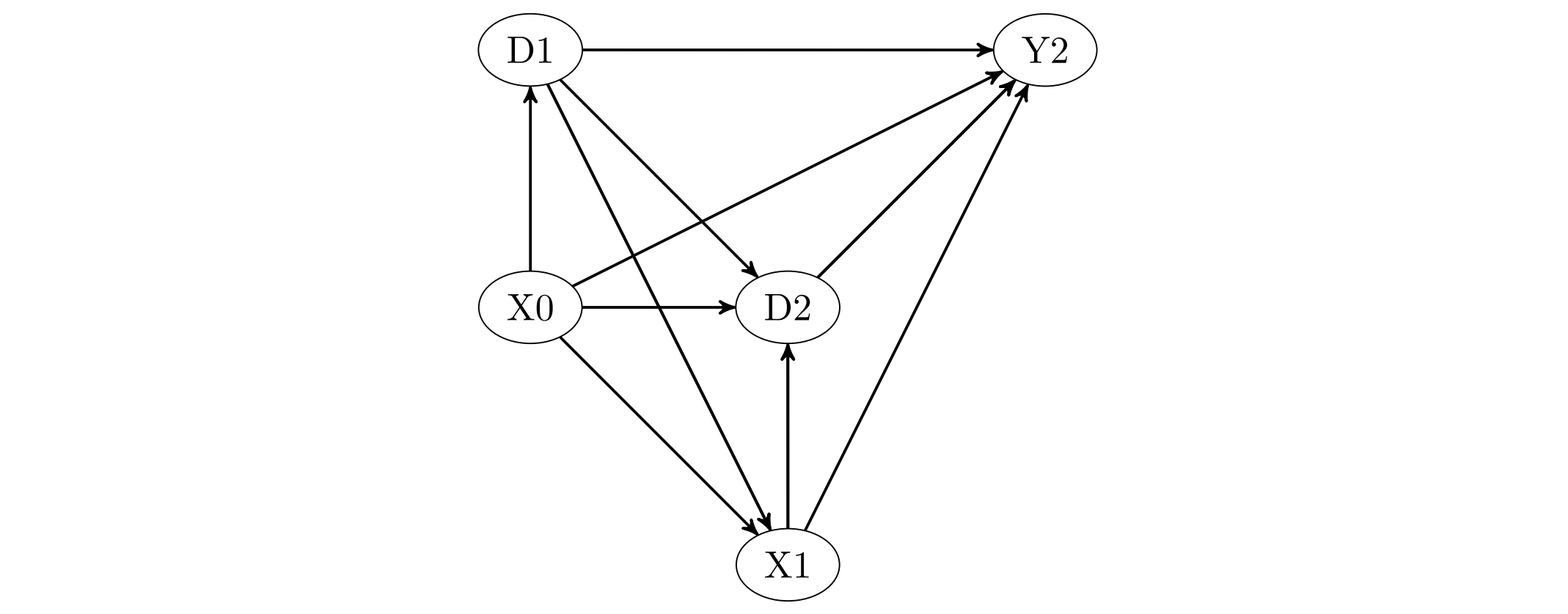
We consider evaluating the causal effects of dynamic treatments, i.e. of multiple treatment sequences in various periods, based on double machine learning to control for observed, time-varying covariates in a data-driven way under a selection-on-observables assumption. To this end, we make use of so-called Neyman-orthogonal score functions, which imply the robustness of treatment effect estimation to moderate (local) misspecifications of the dynamic outcome and treatment models. This robustness property permits approximating outcome and treatment models by double machine learning even under high dimensional covariates and is combined with data splitting to prevent overfitting. In addition to effect estimation for the total population, we consider weighted estimation that permits assessing dynamic treatment effects in specific subgroups, e.g. among those treated in the first treatment period. We demonstrate that the estimators are asymptotically normal and $\sqrt{n}$-consistent under specific regularity conditions and investigate their finite sample properties in a simulation study. Finally, we apply the methods to the Job Corps study in order to assess different sequences of training programs under a large set of covariates.
翻译:我们考虑评估动态治疗的因果关系,即不同时期的多重治疗序列的因果关系,基于双机学习,以可观察、可观察和可观察的假设,以数据驱动的方式,根据双机学习,对观察到的、时间变化的共变情况进行控制;为此,我们使用所谓的Neyman-orthogoal评分功能,这意味着对动态结果和治疗模型的中(当地)误差的治疗效果估计具有稳健性。这种稳健性属性允许即使在高维变量下进行双机学习,以近似结果和治疗模型,并与数据分离相结合,以防止过度匹配。除了对总人口进行估计外,我们考虑加权估计,允许评估特定分组的动态治疗效果,例如,在第一个治疗期接受治疗的分组。我们证明,在特定常规条件下,估计者处于静态正常状态,而美元/qrt{n}$相容,并在模拟研究中调查其有限的抽样特性。最后,我们将这种方法应用于工作团研究,以便评估大型共同培训方案的不同序列。