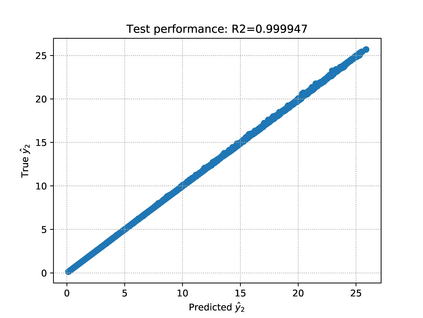
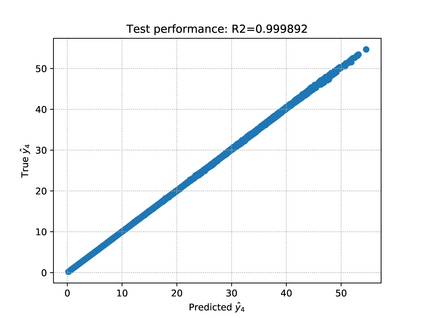
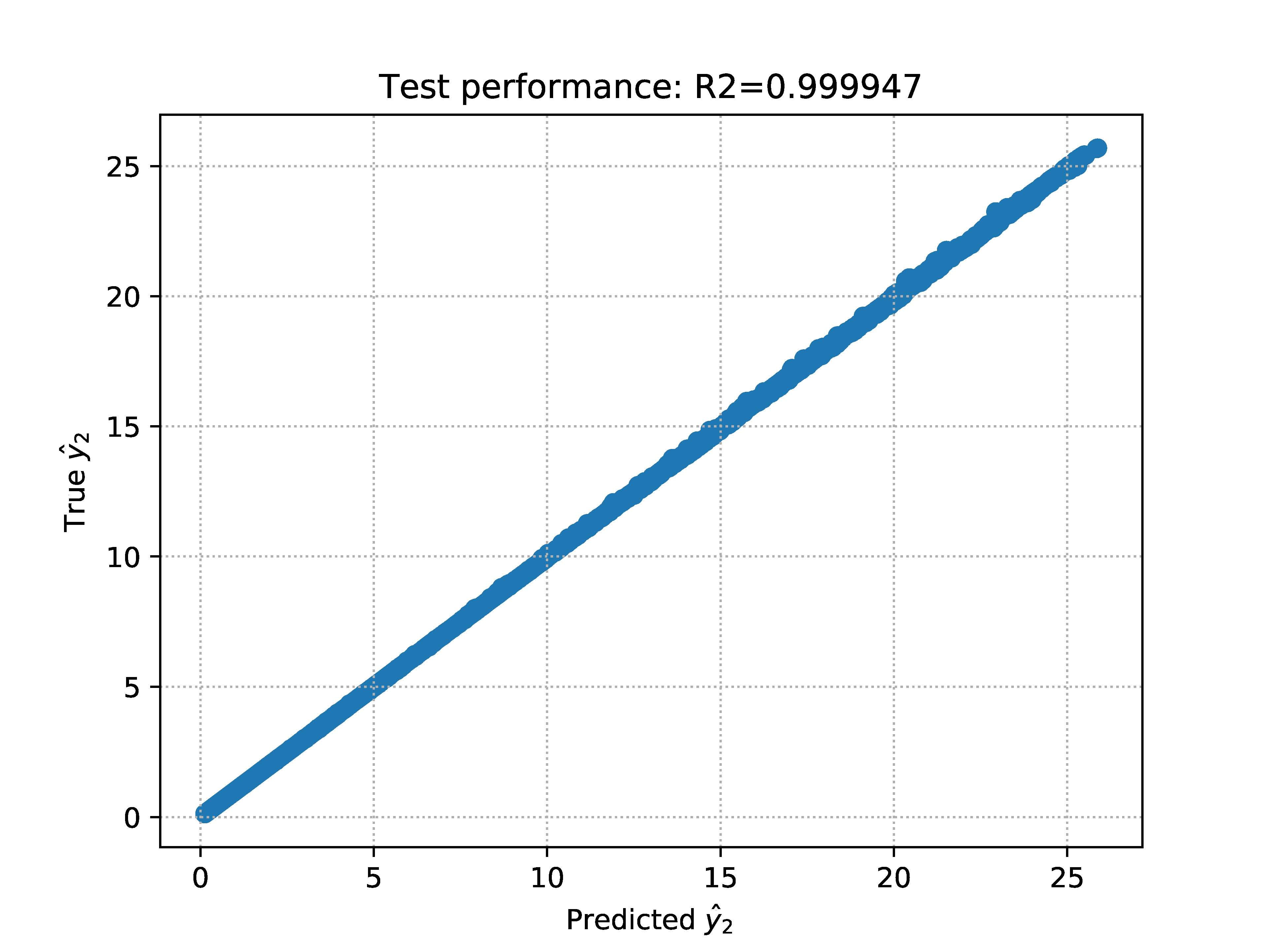
We propose an accurate data-driven numerical scheme to solve Stochastic Differential Equations (SDEs), by taking large time steps. The SDE discretization is built up by means of a polynomial chaos expansion method, on the basis of accurately determined stochastic collocation (SC) points. By employing an artificial neural network to learn these SC points, we can perform Monte Carlo simulations with large time steps. Error analysis confirms that this data-driven scheme results in accurate SDE solutions in the sense of strong convergence, provided the learning methodology is robust and accurate. With a method variant called the compression-decompression collocation and interpolation technique, we can drastically reduce the number of neural network functions that have to be learned, so that computational speed is enhanced. Numerical experiments confirm a high-quality strong convergence error when using large time steps, and the novel scheme outperforms some classical numerical SDE discretizations. Some applications, here in financial option valuation, are also presented.
翻译:我们提出一个精确的数据驱动数字方案,通过采取大量时间步骤解决蒸馏式差异(SDEs) 。 SDE 分散化是通过一种多元混乱扩展方法,在精确确定的蒸馏式合用点(SC)的基础上建立起来的。通过使用人工神经网络来学习这些SC点,我们可以用大的时间步骤进行蒙特卡洛模拟。错误分析证实,这一数据驱动方案的结果是精确的SDE解决方案,其含义是强烈的趋同,条件是学习方法是稳健和准确的。如果使用一种称为压缩-脱压缩合用法和内推法的方法变异,我们可以大幅降低必须学习的神经网络功能的数量,从而提高计算速度。数字实验证实,在使用大的时间步骤时,高品质的强烈趋同差,而新办法则超越了某些典型的数字SDE离化。在财务选项估值中的一些应用也得到了介绍。