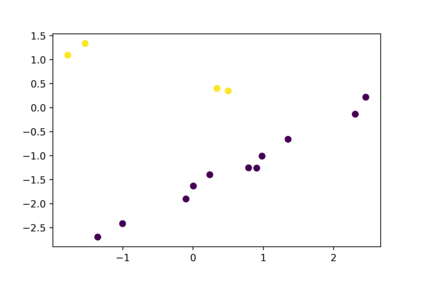
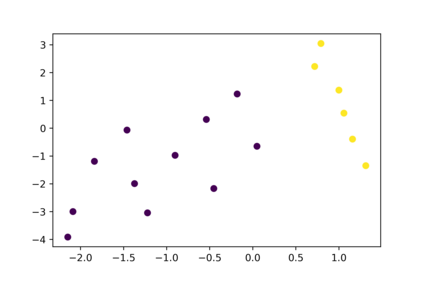
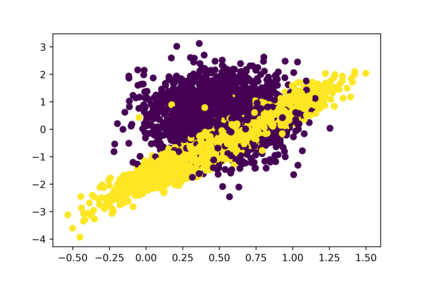
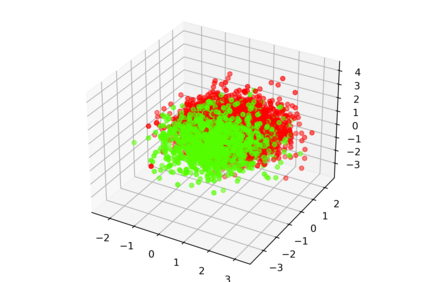
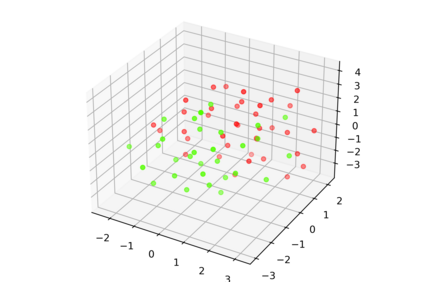
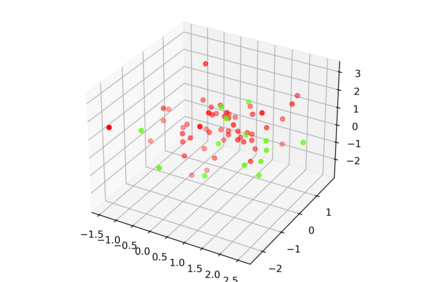
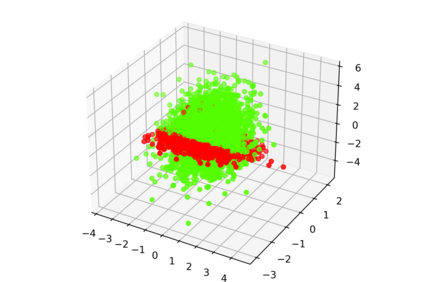
One of the main drawbacks of the practical use of neural networks is the long time required in the training process. Such a training process consists of an iterative change of parameters trying to minimize a loss function. These changes are driven by a dataset, which can be seen as a set of labelled points in an n-dimensional space. In this paper, we explore the concept of are representative dataset which is a dataset smaller than the original one, satisfying a nearness condition independent of isometric transformations. Representativeness is measured using persistence diagrams (a computational topology tool) due to its computational efficiency. We prove that the accuracy of the learning process of a neural network on a representative dataset is "similar" to the accuracy on the original dataset when the neural network architecture is a perceptron and the loss function is the mean squared error. These theoretical results accompanied by experimentation open a door to reducing the size of the dataset to gain time in the training process of any neural network.
翻译:实际使用神经网络的主要缺点之一是培训过程需要很长的时间。这样的培训过程包括迭代改变参数,试图尽量减少损失功能。这些变化是由数据集驱动的,该数据集可以被视为一个维空间的一组标记点。在本文中,我们探讨代表性数据集的概念,该数据集小于原始数据集,符合不因等度变换而存在的近距离状态。由于计算效率高,因此用持久性图表(计算表层工具)来衡量代表性。我们证明,在有代表性的数据集上神经网络的学习过程的准确性与原始数据集的准确性“相似”,当神经网络结构是一个分辨器时,损失函数是平均的方差。这些理论结果伴随着实验,打开了缩小数据集大小的大门,以便在任何神经网络的培训过程中获得时间。