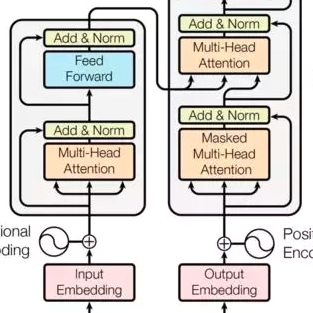
Recent theoretical results show transformers cannot express sequential reasoning problems over long inputs, intuitively because their computational depth is bounded. However, prior work treats the depth as a constant, leaving it unclear to what degree bounded depth may suffice for solving problems over short inputs, or how increasing the transformer's depth affects its expressive power. We address these questions by analyzing transformers whose depth can grow minimally with context length $n$. We show even highly uniform transformers with depth $Θ(\log n)$ can express two important problems: recognizing regular languages, which captures state tracking abilities and was known to be expressible only by an unconventional, non-uniform model of transformers, and graph connectivity, which underlies multi-step reasoning. Notably, both of these problems cannot be expressed by fixed-depth transformers under standard complexity conjectures, demonstrating the expressivity benefit of growing depth. Moreover, our theory quantitatively predicts how depth must grow with input length to express these problems, showing that depth scaling is more efficient than scaling width or chain-of-thought steps. Empirically, our detailed experiments designed to bridge the expressivity vs. learnability gap reveal that our theoretical depth requirements for regular language recognition closely match the practical depth requirements for successfully training transformers. Thus, our results clarify how depth affects a transformer's reasoning capabilities, and provide practical guidance for effective depth selection for sequential reasoning.
翻译:近期理论研究表明,Transformer无法表达对长输入序列的时序推理问题,直观上是因为其计算深度存在上界。然而,先前研究将深度视为常数,未能阐明有限深度在多大程度上足以处理短输入问题,亦未明确增加Transformer深度如何影响其表达能力。本文通过分析深度可随上下文长度$n$最小化增长的Transformer模型来探讨这些问题。我们证明,即使深度仅为$Θ(\log n)$的高度均匀Transformer,也能表达两个关键问题:识别正则语言(该能力对应状态追踪功能,此前仅知可通过非常规非均匀Transformer模型实现)和图连通性判定(该问题是多步推理的基础)。值得注意的是,在标准复杂度假设下,这两个问题均无法由固定深度Transformer表达,这证明了增长深度带来的表达能力优势。此外,我们的理论定量预测了表达这些问题所需深度随输入长度的增长规律,表明深度扩展比扩展宽度或思维链步骤更高效。在实证方面,我们设计了弥合表达能力与可学习性差距的详细实验,结果显示正则语言识别的理论深度要求与成功训练Transformer的实际深度需求高度吻合。因此,本研究阐明了深度如何影响Transformer的推理能力,并为序列推理任务的有效深度选择提供了实践指导。