Why we couldn't prove SETH hardness of the Closest Vector Problem for even norms, and of the Subset Sum Problem!

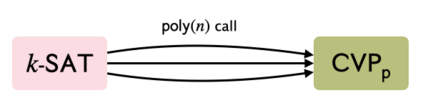
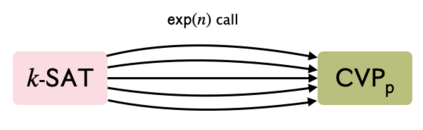
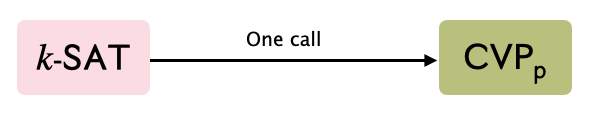Recent work [BGS17,ABGS19] has shown SETH hardness of some constant factor approximate CVP in the $\ell_p$ norm for any $p$ that is not an even integer. This result was shown by giving a Karp reduction from $k$-SAT on $n$ variables to approximate CVP on a lattice of rank $n$. In this work, we show a barrier towards proving a similar result for CVP in the $\ell_p$ norm where $p$ is an even integer. We show that for any $c, c'>0$, if for every $k > 0$, there exists an efficient reduction that maps a $k$-SAT instance on $n$ variables to a $(1+exp(-n^c)))$-CVP instance for a lattice of rank at most $n^{c'}$ in the Euclidean norm, then $\mathsf{coNP} \subset \mathsf{NP/Poly}$. We prove a similar result for $(1+exp(-n^c)))$-CVP for all even norms under a mild additional promise that the ratio of the distance of the target from the lattice and the shortest non-zero vector in the lattice is bounded by $exp(n^{O(1)})$. Furthermore, we show that for any $c,c' > 0$, and any even integer $p$, if for every $k > 0$, there exists an efficient reduction that maps a $k$-SAT instance on $n$ variables to a $(1+exp(-n^c)))$-$SVP_p$ instance for a lattice of rank at most $n^{c'}$, then $\mathsf{coNP} \subset \mathsf{NP/Poly}$. The result for SVP does not require any additional promise. While prior results have indicated that lattice problems in the $\ell_2$ norm (Euclidean norm) are easier than lattice problems in other norms, this is the first result that shows a separation between these problems. We achieve this by using a result by Dell and van Melkebeek [JACM, 2014] on the impossibility of the existence of a reduction that compresses an arbitrary $k$-SAT instance into a string of length $\mathcal{O}(n^{k-\epsilon})$ for any $\epsilon>0$. In addition to CVP, we also show that the same result holds for the Subset-Sum problem using similar techniques.