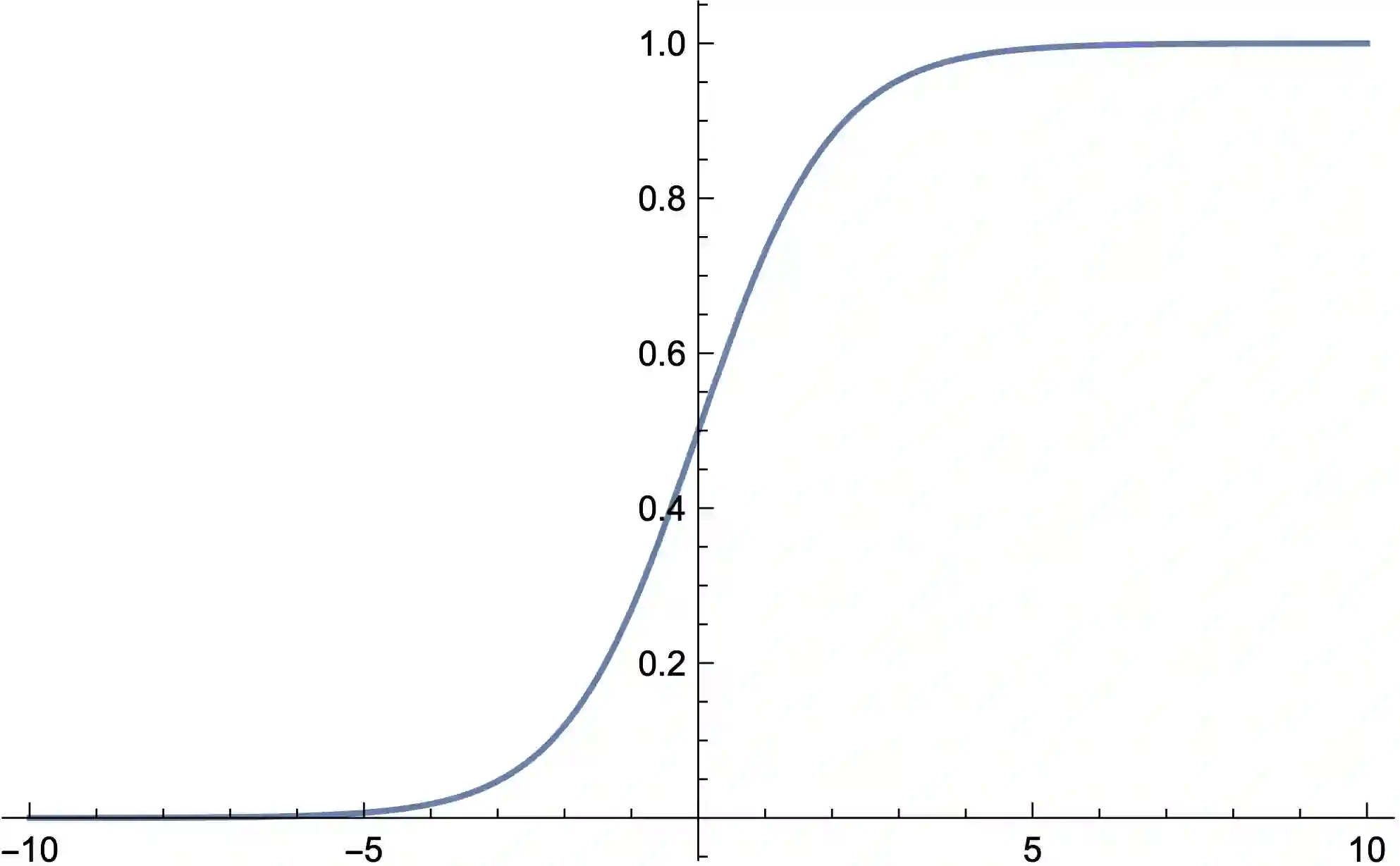
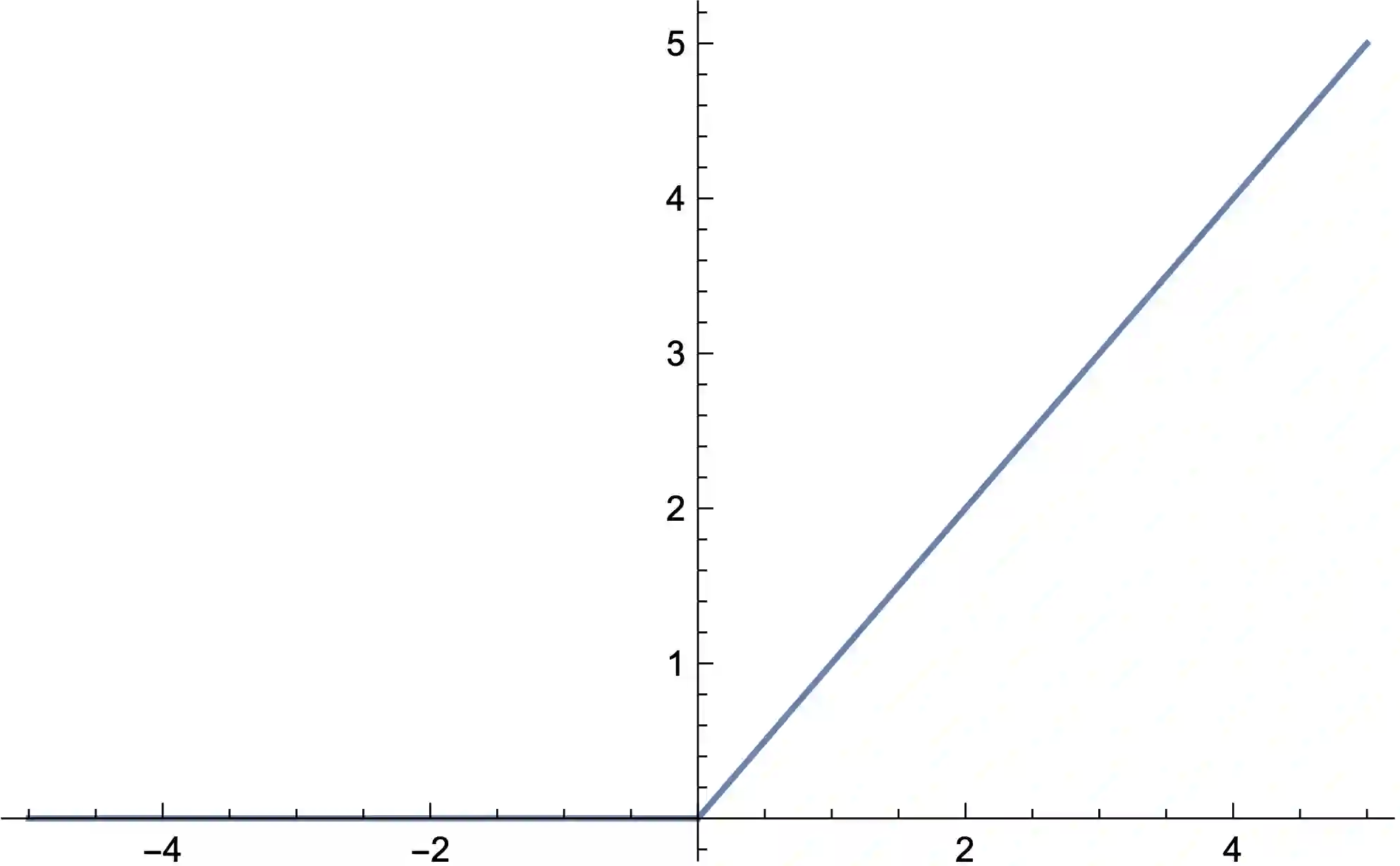
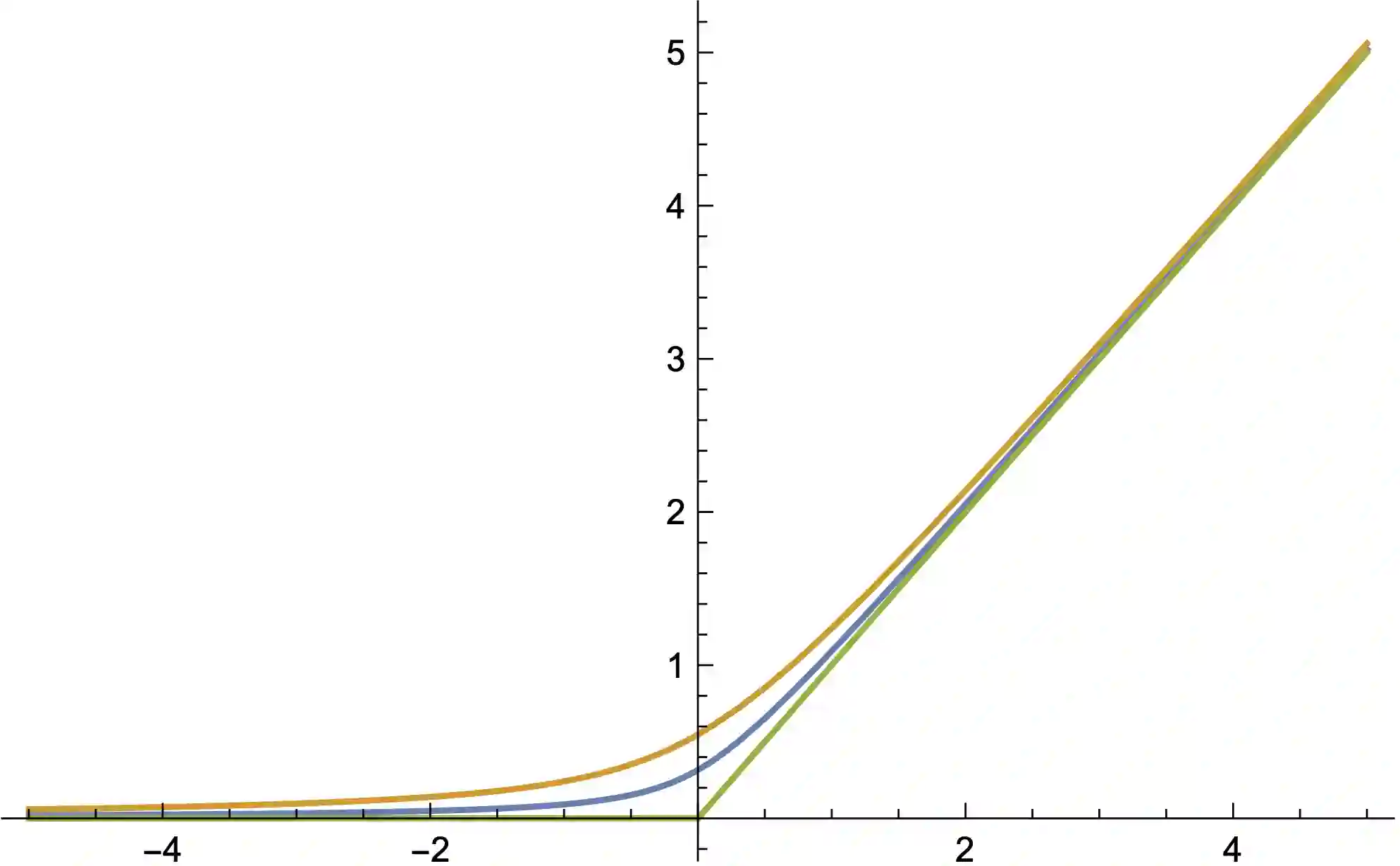
This paper is concerned with the utilization of deterministically modeled chemical reaction networks for the implementation of (feed-forward) neural networks. We develop a general mathematical framework and prove that the ordinary differential equations (ODEs) associated with certain reaction network implementations of neural networks have desirable properties including (i) existence of unique positive fixed points that are smooth in the parameters of the model (necessary for gradient descent), and (ii) fast convergence to the fixed point regardless of initial condition (necessary for efficient implementation). We do so by first making a connection between neural networks and fixed points for systems of ODEs, and then by constructing reaction networks with the correct associated set of ODEs. We demonstrate the theory by constructing a reaction network that implements a neural network with a smoothed ReLU activation function, though we also demonstrate how to generalize the construction to allow for other activation functions (each with the desirable properties listed previously). As there are multiple types of "networks" utilized in this paper, we also give a careful introduction to both reaction networks and neural networks, in order to disambiguate the overlapping vocabulary in the two settings and to clearly highlight the role of each network's properties.
翻译:本文涉及利用确定模型化化学反应网络实施(feed-forward)神经网络的问题。我们开发了一个一般数学框架,并证明与神经网络的某些反应网络实施有关的普通差分方程式具有可取的特性,包括:(一) 存在独特的正值固定点,这些点在模型参数参数中是顺畅的(梯度下降所必需的),以及(二) 快速接近固定点,而不论初始条件如何(有效实施的必要条件),我们这样做的办法是首先在神经网络和ODE系统的固定点之间建立联系,然后与正确的一套相关的ODE建立反应网络。我们通过建立一个反应网络来展示这一理论,这个网络运行一个神经网络,具有平滑的ReLU激活功能,但我们也展示了如何将构造加以推广,以允许其他激活功能(每一个都使用先前列出的可取特性)。由于本文件使用了多种类型的“网络”,因此我们还要仔细介绍两种反应网络和神经网络,以便消除两个环境中的重叠词汇,并明确突出每个网络的作用。