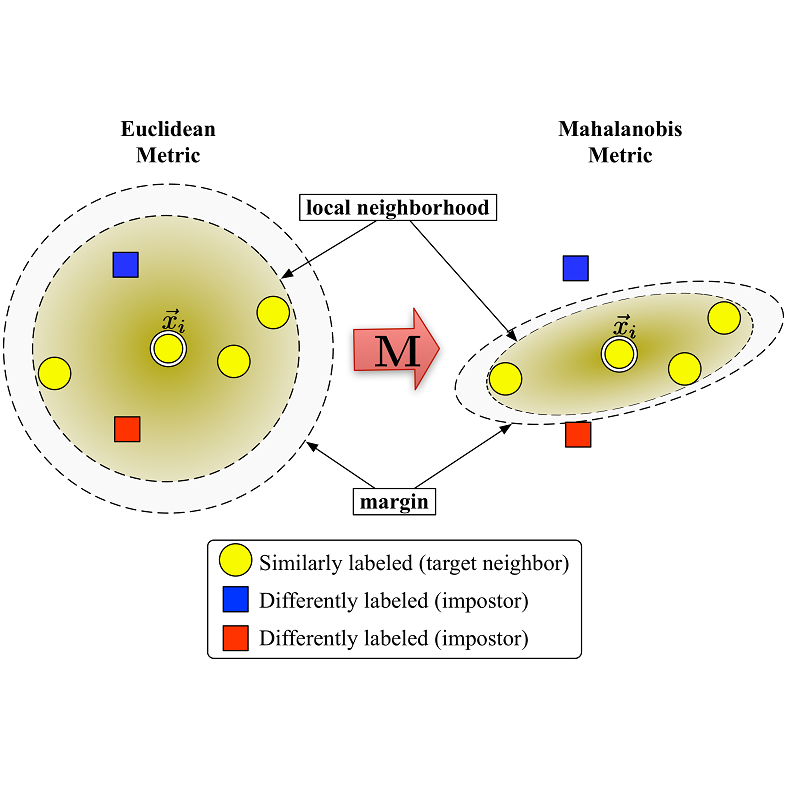
Metric learning is an important family of algorithms for classification and similarity search, but the robustness of learned metrics against small adversarial perturbations is less studied. In this paper, we show that existing metric learning algorithms, which focus on boosting the clean accuracy, can result in metrics that are less robust than the Euclidean distance. To overcome this problem, we propose a novel metric learning algorithm to find a Mahalanobis distance that is robust against adversarial perturbations, and the robustness of the resulting model is certifiable. Experimental results show that the proposed metric learning algorithm improves both certified robust errors and empirical robust errors (errors under adversarial attacks). Furthermore, unlike neural network defenses which usually encounter a trade-off between clean and robust errors, our method does not sacrifice clean errors compared with previous metric learning methods. Our code is available at https://github.com/wangwllu/provably_robust_metric_learning.
翻译:计量学习是分类和类似搜索的重要算法体系,但是,对小对抗性扰动的学习指标的稳健性研究较少。在本文中,我们表明,现有的计量学习算法侧重于提高清洁准确度,但可以产生比欧几里德距离差强得多的计量法。为解决这一问题,我们建议采用新的计量算法,以找到一个能够抵御敌对性扰动的马哈拉诺比距离,而由此形成的模型的稳健性是可验证的。实验结果表明,拟议的计量算法既改进了经认证的稳健错误,也改进了经验强健的错误(在对抗性攻击下的劫机 ) 。 此外,与通常在清洁和稳健错误之间发生权衡的神经网络防御不同,我们的方法并不牺牲与以往的计量学习方法相比的清洁错误。我们的代码可在https://github.com/wanwllu/prove_robust_robust_contran_leiness_lementation_ining.