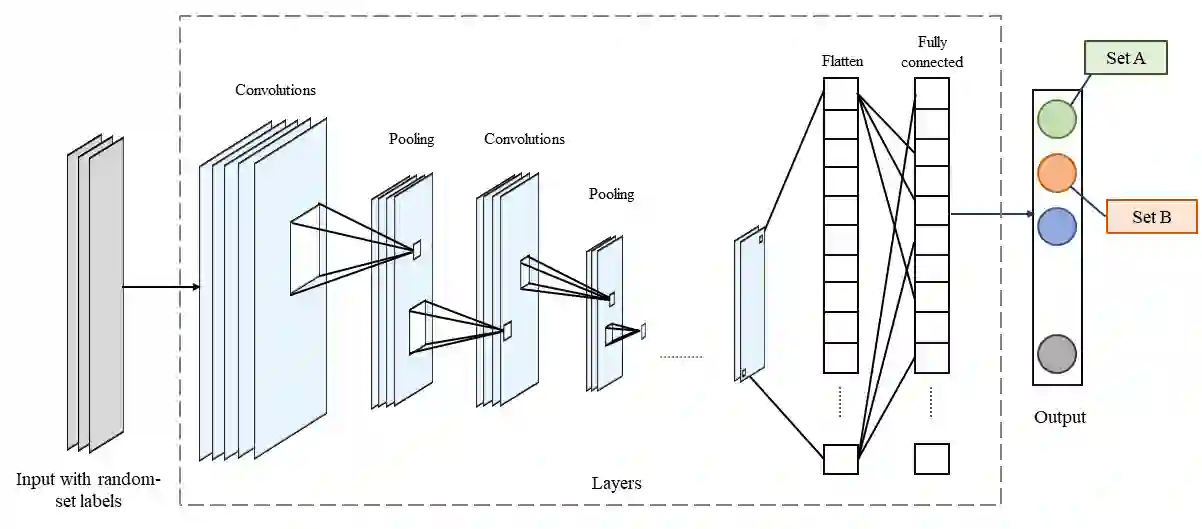
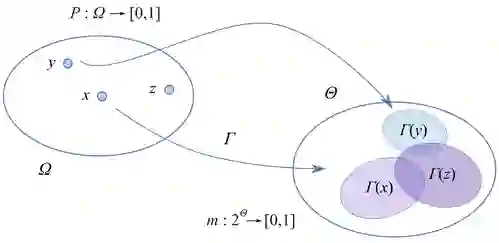
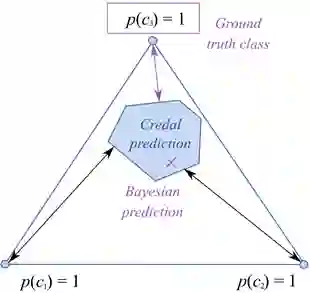
The belief function approach to uncertainty quantification as proposed in the Demspter-Shafer theory of evidence is established upon the general mathematical models for set-valued observations, called random sets. Set-valued predictions are the most natural representations of uncertainty in machine learning. In this paper, we introduce a concept called epistemic deep learning based on the random-set interpretation of belief functions to model epistemic learning in deep neural networks. We propose a novel random-set convolutional neural network for classification that produces scores for sets of classes by learning set-valued ground truth representations. We evaluate different formulations of entropy and distance measures for belief functions as viable loss functions for these random-set networks. We also discuss methods for evaluating the quality of epistemic predictions and the performance of epistemic random-set neural networks. We demonstrate through experiments that the epistemic approach produces better performance results when compared to traditional approaches of estimating uncertainty.
翻译:Demspter-Shafer 证据理论中提议的不确定性量化的信仰功能方法,是根据定值观察的一般数学模型(称为随机集体)确定的。定值预测是机器学习中不确定性的最自然表现。在本文中,我们引入了一个概念,即根据对信仰函数的随机解释进行感知深层次学习,以模拟深神经网络的感知学习。我们提议了一个新颖的随机集成神经神经网络分类网络,通过学习定值地面真象表征,得出各班级分数。我们评估了不同配方的灵敏度和距离测量方法,将信仰功能作为这些随机集成网络的可行损失函数。我们还讨论了评估定数预测质量和成形随机神经网络表现的方法。我们通过实验证明,与传统的估计不确定性的方法相比,定值法方法产生更好的业绩结果。