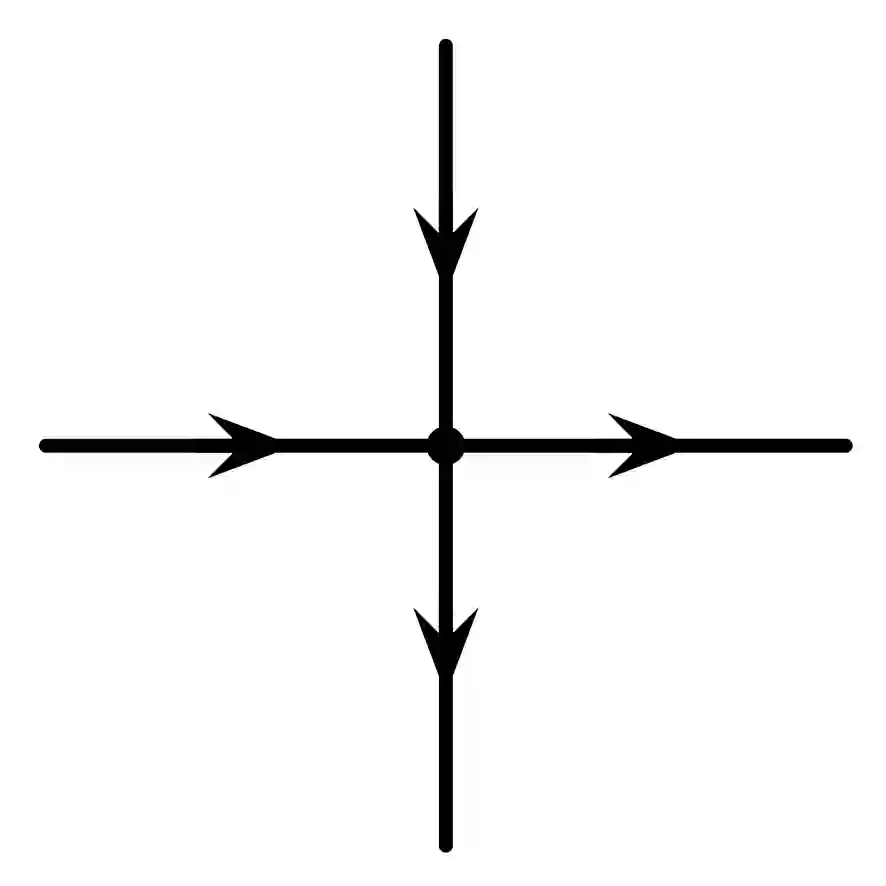
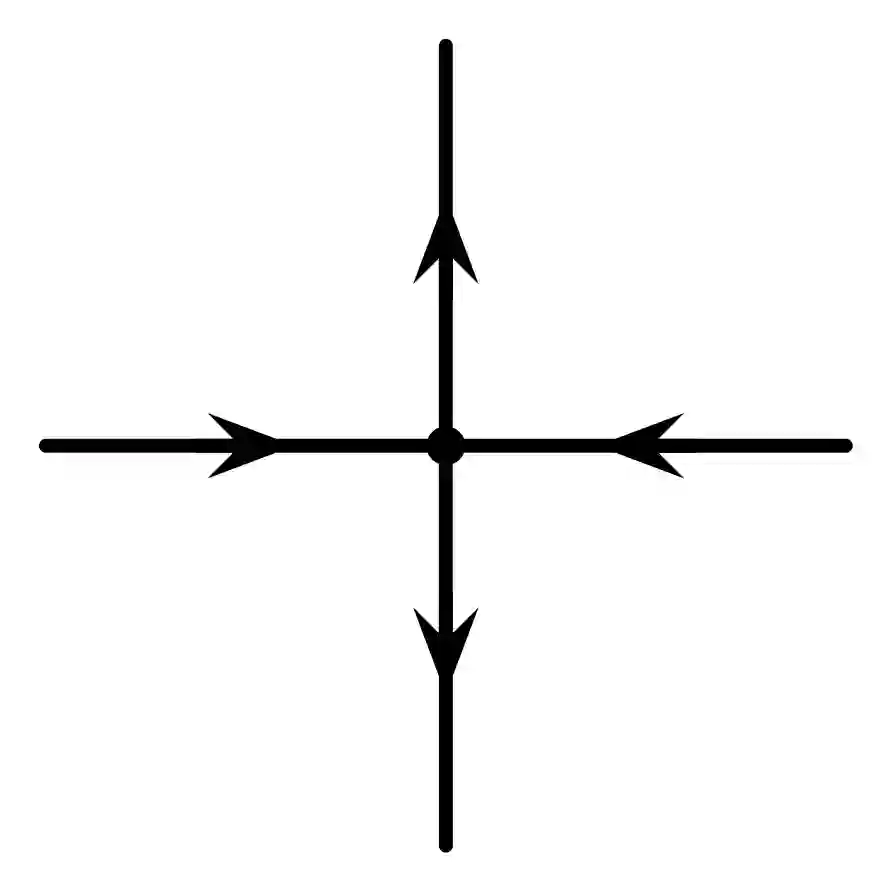
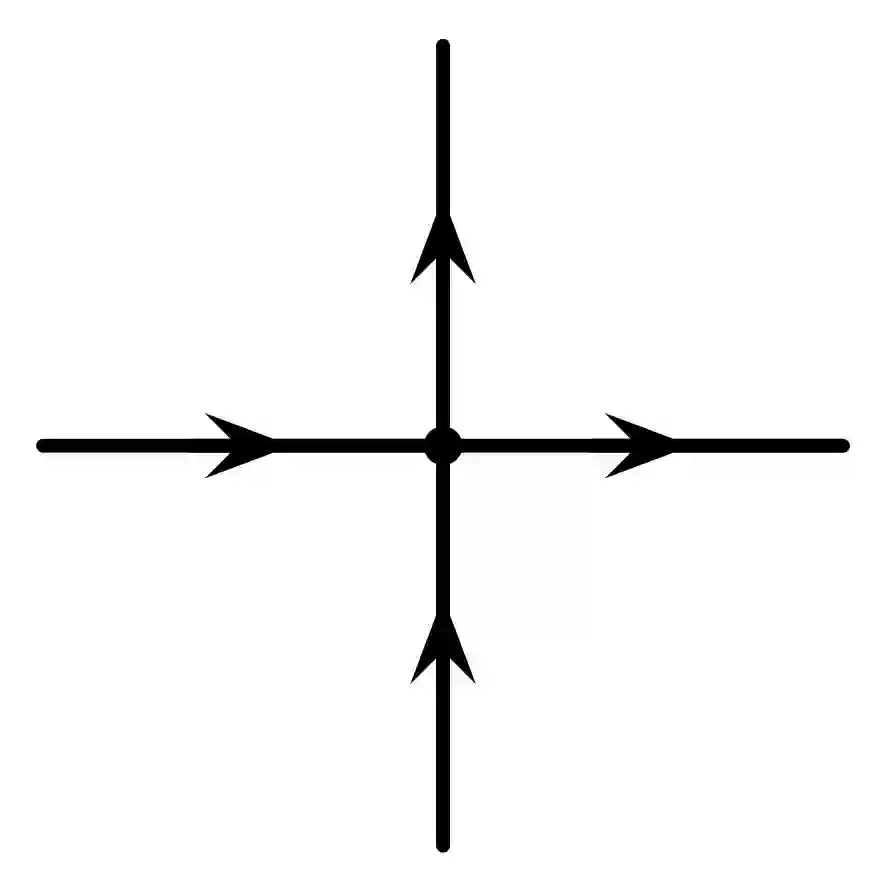
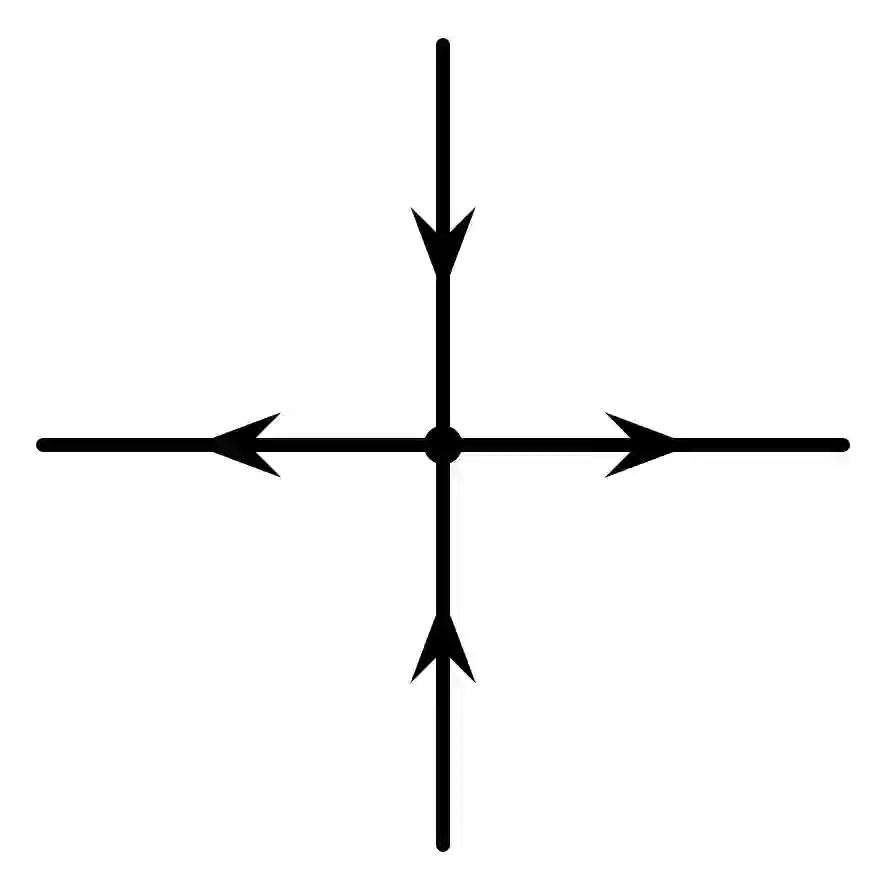
The six-vertex model is an important model in statistical physics and has deep connections with counting problems. There have been some fully polynomial randomized approximation schemes (FPRAS) for the six-vertex model [30, 10], which all require that the constraint functions are windable. In the present paper, we give an FPRAS for the six-vertex model with an unwindable constraint function by Markov Chain Monte Carlo method (MCMC). Different from [10], we use the Glauber dynamics to design the Markov Chain depending on a circuit decomposition of the underlying graph. Moreover, we prove the rapid mixing of the Markov Chain by coupling, instead of canonical paths in [10].
翻译:6个顶点模型是统计物理学中的一个重要模型,与计算问题有着深刻的联系。对于6个顶点模型[30、10],已经有一些完全的多元随机近似方案(FPRAS),所有这些方案都要求制约功能是可变的。在本文件中,我们给6个顶点模型一个FPRAS,由Markov Cain Monte Carlo方法(MCMC)提供一种不可变的制约功能。与[10]不同,我们使用Glauber动力来设计Markov链条,这取决于基本图的电路分解。此外,我们证明Markov链条通过联结而不是用10(10)的金路快速混合。