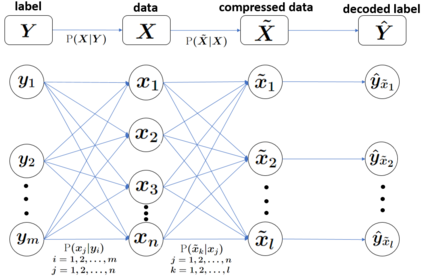
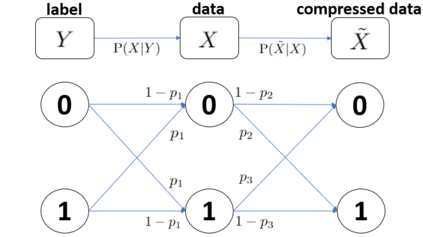
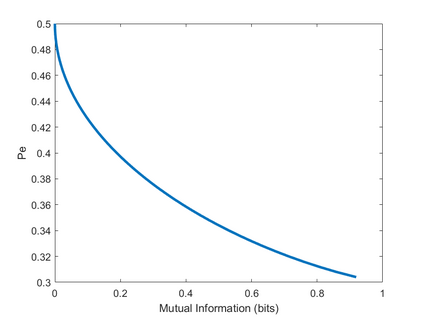
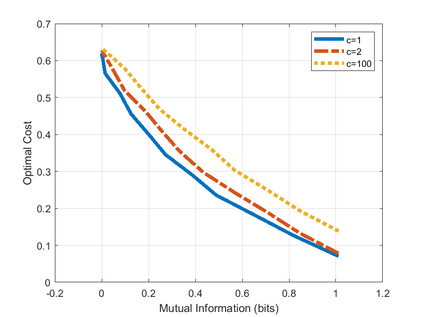
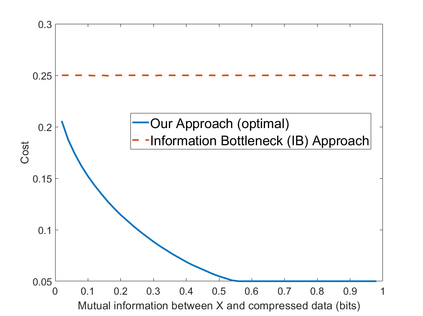
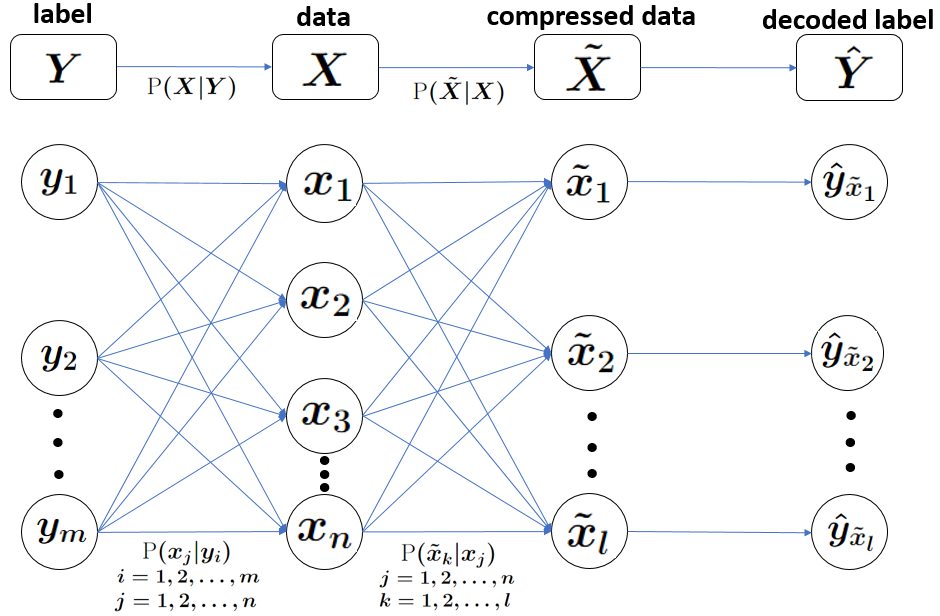
We formulate the problem of performing optimal data compression under the constraints that compressed data can be used for accurate classification in machine learning. We show that this translates to a problem of minimizing the mutual information between data and its compressed version under the constraint on error probability of classification is small when using the compressed data for machine learning. We then provide analytical and computational methods to characterize the optimal trade-off between data compression and classification error probability. First, we provide an analytical characterization for the optimal compression strategy for data with binary labels. Second, for data with multiple labels, we formulate a set of convex optimization problems to characterize the optimal tradeoff, from which the optimal trade-off between the classification error and compression efficiency can be obtained by numerically solving the formulated optimization problems. We further show the improvements of our formulations over the information-bottleneck methods in classification performance.
翻译:我们提出在压缩数据可用于机器学习准确分类的限制下进行最佳数据压缩的问题。我们指出,这说明在使用压缩数据进行机器学习时,在使用压缩数据进行最佳权衡和分类误差概率的限制下,尽量减少数据与压缩版本之间的相互信息的问题。我们然后提供分析和计算方法,说明数据压缩和分类误差概率的最佳取舍。首先,我们为二元标签数据的最佳压缩战略提供分析特征描述。第二,对于多标签数据,我们提出一套convex优化问题,以说明最佳取舍的特点,从而通过用数字解决所提出的优化问题,实现分类误差与压缩效率的最佳取舍。我们进一步展示了我们在分类性能方面对信息瓶式方法的改进。